Операционные усилители, страница 4

Как видно из этих выражений напряжение на нагрузке прямо пропорционально сопротивлению нагрузки, а ток в нагрузке  не зависит (в рамках принятых допущений) от R_н. что и является признаком токового выхода.

2. ПРИМЕНЕНИЕ ОУ В АНАЛОГОВЫХ СХЕМАХ ОБРАБОТКИ СИГНАЛОВ

2.1. Фазовращатели

Фазовращатель позволяет задать на определенной частоте необходимый фазовый сдвиг между входным и выходным напряжениями без изменения модуля функции передачи. Зная передаточные функции с инвертирующего и не инвертирующего входов ОУ охваченного отрицательной обратной связью, найдем выражения функций передачи фазовращателей, схемы которых приведены на рис. 6,а и б:

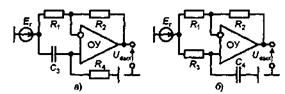
Рис 6. Фазовращатели на ОУ
 а - с положительной фазой, б - с отрицательной фазой

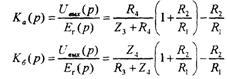
Если R₂ =R₁ то эти функции примут следующий вид

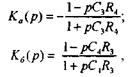
а выражения амплитудно-частотных и фазо-частотных характеристик:

.

Таким образом, схемы на рис. 6 можно использовать в качестве фазовых корректоров, у которых модуль функции передачи в широком диапазоне частот (где операционный усилитель можно считать идеальным) не зависит от частоты.

2.2. Интеграторы

Операцию интегрирования можно реализовать путем линейного заряда и разряда конденсатора для чего требуется источник тока с достаточно большим (в идеале – бесконечным) сопротивлением. Схему интегратора можно получить из схемы усилителя с токовым выходом (см рис. 4а и б), если вместо R_н включить конденсатор С, как показано на рис. 7. Чтобы получить несимметричный низкоомный выход, выходной сигнал интегратора можно снимать не с конденсатора, а с выхода ОУ. Но напряжение на выходе ОУ и напряжение на конденсаторе (с точностью до масштабного коэффициента) совпадают только в том случае, когда входной сигнал в схеме рис. 7а подается на инвертирующий вход ОУ, а в схеме рис 76 -на не инвертирующий вход.

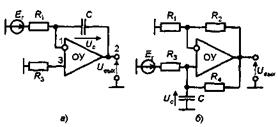
Рис.3.5 Интеграторы: а - инвертирующий,  б - неинвертируюший

В схеме рис. 7а U_tвых =U_с (напряжение в узле 1 близко к нулю), а в схеме рис. 76 U_вых=U_c(1+R₂/R_l) (т.е. U_c усиливается не инвертирующим усилителем), выходного напряжения интеграторов можно выразить из формулы (4), заменив R_н на Z =1/pC :

Перейдя от изображений к оригиналам, получим

Отсюда коэффициенты передачи инвертирующего и не инвертирующего интеграторов соответственно равны

амплитудно-частотная и фазочастотная характеристики интеграторов определятся выражениями

где k_м=1, t = СR,, j₀ =p для схемы рис. 7а, k_м =1+ R₂/R_l, t = CR₃, j₀ =0 для схемы рис. 7б. Постоянная времени t выбирается, исходя из диапазона частот входного сигнала и требования к величине выходного напряжения. Приведенные выше соотношения получены в предположении идеальности операционного усилителя, а в схеме не инвертирующего интегратора еще и при условии R₁=R₃. R₂=R₄. Если в схеме рис. 7а учесть конечность коэффициента усиления ОУ m, а в схеме рис. 76 - возможные отклонения сопротивлений R_} и R₂ от их расчетных значений, то функции передачи интеграторов примут вид