



§ потери мощности на корону.
Нагрузочные потери мощности являются переменными и зависят от потока мощности, протекающего по элементу. Потери холостого хода и потери на корону – постоянные.
Метод 1.
Расчет потерь в каждом элементе сети можно определить, используя данные из предварительно рассчитанного установившегося режима
Суммарные потери в элементе (i, j) можно легко определить по формуле [1]:
DРS(1, 2 )=P1 – P2, (2.28)
С другой стороны эти же потери можно рассчитать по формуле:
DРS(1, 2)=Р11+Р22+Р12,max(-2sina12cosδ12), (2.29)
или:
DРS(1, 2)=(U12+U22)Y11sina11 – 2U1U2Y12sina12cosδ12, (2.30)
где:
U1, U2 – модуль напряжения соответственно в начале и конце линии;
Y11, Y12 – соответственно собственная и взаимная проводимость линии;
δ12 – разность углов между напряжениями U1 и U2.
Y11sina11=yr+gл/2, (2.31)
Y12sina12=yr. (2.32).
Тогда (2.30) преобразуется к виду
DРS(1, 2)=U12gл/2+U22gл/2+(U12+U22)yr-2U1U2yrcosδ12 (2.33).
Первые два слагаемых в правой части в случае воздушной линии соответствуют потерям на корону:
DРкор= U12gл/2+U22gл/2 (2.34).
Последние два слагаемых в (2.33)
отвечают потерям в активном сопротивлении продольной ветви схемы замещения, т.
е. Потерям на нагрев проводов (DР12), которые являются функцией угла сдвига векторов ![]() и
и ![]() .
Минимальные потери на нагрев имеют место при δ12=0. При этом
в линию поступают одинаковые активные мощности с обеих сторон линии, каждая из
которых идет на покрытие половины потерь на корону.
.
Минимальные потери на нагрев имеют место при δ12=0. При этом
в линию поступают одинаковые активные мощности с обеих сторон линии, каждая из
которых идет на покрытие половины потерь на корону.
Потери мощности в трансформаторах рассчитываются по следующим формулам:
DРтS» nт DРх + ![]() DРк
DРк 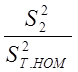 , (2.38)
, (2.38)
где:
DРх, DРк – соответственно потери холостого хода и короткого замыкания в трансформаторе;
nт– количество параллельно работающих трансформаторов;
u*к, I*x – соответственно напряжение короткого замыкания и ток холостого хода, выраженные в процентах от номинала;
Sт. ном – номинальная мощность трансформатора.
Метод 2.
Кроме того, существует метод расчета потерь мощности с использованием известных значений матрицы узловых проводимостей, представленной в декартовой форме, и векторов активной и реактивной составляющих узловых напряжений.
Уравнения установившегося режима можно записать в следующем виде:
![]() U’12
Y’i i+U’i
U’12
Y’i i+U’i![]() (U’j’Y’i j – U”j Y”i j)+U’’i
(U’j’Y’i j – U”j Y”i j)+U’’i![]() (U’j Y”i j+U”j Y’j)+Pнг-Ргi=0
(U’j Y”i j+U”j Y’j)+Pнг-Ргi=0
-U”12
Y”i i+U”i![]() (U’j’Y’i
j – U”j Y”i j)-U’i
(U’j’Y’i
j – U”j Y”i j)-U’i![]() (U’j
Y”i j+U”j Y’j)+Qнг-Qгi=0
(U’j
Y”i j+U”j Y’j)+Qнг-Qгi=0
(2.40).
Активные потери мощности могут быть найдены из баланса мощностей:
p=![]() Рг i -
Рг i - ![]() Рнг i (2.41).
Рнг i (2.41).
После подстановки приведенных выражений и приведения подобных членов, потери активной мощности можно записать:
p=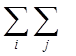 U’i U’jY’i j+
U’i U’jY’i j+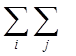 U”i U”jY’i
j (2.42).
U”i U”jY’i
j (2.42).
Или в матричном виде:
p=U’TY’U’+U”TY’U”, (2.43)
после введенных матричных обозначений:
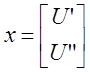 ,
,
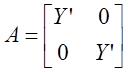 . (2.44)
. (2.44)
Тогда потери активной мощности могут быть записаны следующим образом:
p=хт А х, (2.45)
Рассмотрен алгоритм расчет режима методом поочередного вычисления векторов напряжения и тока.
Приведена структура исходных данных, необходимых для расчета.
Разобраны алгоритмы формирования матрицы узловых проводимостей с учетом трансформаторных ветвей и ортогонально-треугольного разложения.
Приведен алгоритм и блок-схема расчета установившегося режима в декартовой системе координат.
Рассмотрены методы расчета потерь активной мощности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.