Теория вероятностей: Случайные величины. Материалы к самостоятельной работе студентов

1.  Введение

    В деятельности современного специалиста есть стороны, которые носят научно-исследовательский характер. Одним из этапов самостоятельной научно-исследовательской работы студентов педагогического колледжа является выполнение курсовых и выпускных квалификационных (дипломных) работ. Выполнение дипломных работ предусмотрено Государственным образовательным стандартом среднего профессионального образования как обязательный вид итоговой аттестации студентов. В этой связи подготовка дипломных работ в колледже из средства развития творческих способностей наиболее одаренных студентов превращается в средство повышения качества подготовки всех специалистов со средним педагогическим образованием, т.е. приобретает массовый характер. Поэтому вопросы методологического обеспечения организации и проведения этой важнейшей работы имеет большую значимость.

     Студенты в процессе освоения профессиональной образовательной программы должны овладеть основными методами научно-педагогических исследований, научиться обрабатывать количественные данные, полученные в результате наблюдений, анкетирования, экспериментов, анализировать их и строить прогноз при помощи математических статистических методов.

     Успешному изучению математической статистики, как в рамках дисциплины «Математика» так и в рамках факультативного курса «Основы математической статистики», способствует знание студентами основных понятий и методов теории вероятностей.      В данном методическом пособии представлены   базовые теоретические вопросы с практическими примерами по ключевому разделу теории вероятностей «Случайная величина: закон распределения, числовые характеристики». Данное пособие, несомненно, окажет помощь студенту при самостоятельной работе,   как в процессе изучения указанных дисциплин, так и при выполнении учебно-исследовательских работ (курсовой, выпускной квалификационной).

2.  Основные виды  измерительных шкал

     Проведение любых исследований связано с определенными измерениями. Измерение в самом широком смысле может быть определено как приписывание чисел к объектам или событиям согласно некоторым правилам. Эти правила должны устанавливать соответствие между свойствами рассматриваемых объектов и числами, что порождает четыре основных вида шкал:

·  наименований;

·  порядка;

·  интервальная;

·  отношений.

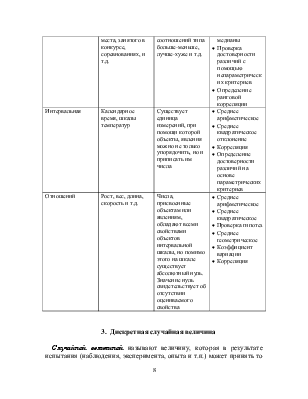
 Измерения, осуществляемые с помощью двух первых шкал, считаются качественными, двух последних – количественными. В  каждой шкале строго определены свойства чисел, приписываемых объектам. При  этом, чем выше порядок шкалы, тем больше арифметических действий разрешается проводить с этими числами.

2.1.  Шкала наименований

Построение этой шкалы основано на группировке объектов, явлений в соответствующие классы в зависимости от проявления у них определенных признаков или свойств. Всем объектам или явлениям, попавшим в один и тот же класс или группу, приписывается одно и то же число, объектам и явлениям другого класса – другое число.

Пример. Всех студентов в зависимости от того, каким игровым видом спорта занимаются, можно подразделить на следующие классы:

·  баскетболисты;

·  волейболисты;

·  футболисты.

В данном случае каждому классу можно приписать числа:

классу баскетболистов – 1, классу волейболистов – 2, классу футболистов – 3. В результате студенты будут отнесены к тому или иному классу, группе специализаций.

      Таким образом, изучаемые объекты можно подразделить на определенные классы  в зависимости от пола, возраста, разряда, принадлежности к тому или иному сообществу, клубу, партии и т.п.

      Условием применения шкалы наименований является наличие критерия, с помощью которого  исследователь может однозначно отличить один объект, который имеет необходимый признак или свойство,  от другого, который его не имеет. Приписывание чисел в этом случае производится произвольно, и их величина и порядок не имеют никакого значения. Они используются только в качестве ярлыков, позволяющих отличить один класс от другого. Такие числа можно заменить любыми другими символами – буквами, звездочками и т.п.

     Количественная обработка экспериментальных данных проводится не с самими приписываемыми числам, а с числами, характеризующими количество объектов, попавших в каждый класс. Допустимыми статистическими операциями будут:

·  подсчет числа объектов в каждом классе;

·  выявление простого или процентного отношения числа объектов в каждом классе к общему числу рассматриваемых объектов;

·  применение полученных выше результатов для проверки некоторых статистических гипотез, вычисления показателей корреляции качественных признаков.

2.2.  Шкала порядка

    Порядковые измерения (ранжирование) возможны тогда, когда исследователь может обнаружить в объектах или явлениях различие степеней признака или свойства и на этой основе расположить эти объекты в порядке возрастания или убывания величины рассматриваемого признака или свойства. Каждому объекту или явлению в этом случае приписывается порядковое число, обозначающее его место в данном ряду. Это число называется рангом.