50
 В первой половине 19 века почти
всеобщее признание получила точка зрения, согласно которой
изменения поля происходит одновременно с изменением тока, а это
равносильно предположению о мгновенной “передаче” изменения
из точки М в точку А без участия промежуточной среды (
В первой половине 19 века почти
всеобщее признание получила точка зрения, согласно которой
изменения поля происходит одновременно с изменением тока, а это
равносильно предположению о мгновенной “передаче” изменения
из точки М в точку А без участия промежуточной среды (![]() большой скорости передачи). Отсюда название такой “передачи” действия
на расстоянии – дальнодействие. Иные взгляды отстаивали сторонники теории
близкодействия, т. е
передачи изменений с конечной скоростью.
Огромную роль при обосновании этой теории сыграло введение Максвеллом локальных
величин и процессов, относящихся к
большой скорости передачи). Отсюда название такой “передачи” действия
на расстоянии – дальнодействие. Иные взгляды отстаивали сторонники теории
близкодействия, т. е
передачи изменений с конечной скоростью.
Огромную роль при обосновании этой теории сыграло введение Максвеллом локальных
величин и процессов, относящихся к ![]() малым V, к
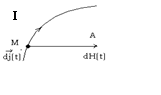
точкам. Согласно Фарадею и Максвеллу, изменение тока в
точке М вызывает изменение поля в прилегающих точках, V3. Это изменение вызывыает изменение поля в соседнем с ним точках , и, таким
образом, начальное изменение в виде некоторого волнового ЭМ
процесса передается от точки к точки пока не дойдет до точки наблюдения А.
Воздействие процесса в одной точке на процесс в соседней, то
есть передача сигнала, происходит с конечной скоростью u, поэтому
изменение поля в точке А произойдет позже, чем его причина
– изменение тока в точке М; время запаздывания
малым V, к
точкам. Согласно Фарадею и Максвеллу, изменение тока в
точке М вызывает изменение поля в прилегающих точках, V3. Это изменение вызывыает изменение поля в соседнем с ним точках , и, таким
образом, начальное изменение в виде некоторого волнового ЭМ
процесса передается от точки к точки пока не дойдет до точки наблюдения А.
Воздействие процесса в одной точке на процесс в соседней, то
есть передача сигнала, происходит с конечной скоростью u, поэтому
изменение поля в точке А произойдет позже, чем его причина
– изменение тока в точке М; время запаздывания ![]() t=
t=![]() . Запаздывание было экспериментально доказано Герцем,
воспользовавшимся для этой цели быстро перемещающимися токами (токами высокой
частоты). В переменном поле
значения потенциалов и векторов поля в данный момент времени t определяется тем распределением величин,
которые существовали в некотором предшествующем моменте времени t -
. Запаздывание было экспериментально доказано Герцем,
воспользовавшимся для этой цели быстро перемещающимися токами (токами высокой
частоты). В переменном поле
значения потенциалов и векторов поля в данный момент времени t определяется тем распределением величин,
которые существовали в некотором предшествующем моменте времени t -![]() t = t -
t = t - ![]() . Однако сеществоеание переменного поля к которым в первом приближении
приложимы законы стационарных полей; соответствующие им переменные
токи можно рассматривать как стационарные. Такие токи и
поля называются квазистационарными. Сформулируем условия, при
котором переменные токи и их поля можно считать квазист-ми.
. Однако сеществоеание переменного поля к которым в первом приближении
приложимы законы стационарных полей; соответствующие им переменные
токи можно рассматривать как стационарные. Такие токи и
поля называются квазистационарными. Сформулируем условия, при
котором переменные токи и их поля можно считать квазист-ми.
1.
Переменные токи должны в каждый
момент времени обладать одинаковой величиной во всех участках неразветвленной
цепи, иначе говоря, колебания тока во всех точках
линии должны совпадать по фазе; это условие означает, что длина линии
должна быть малой по сравнению с длиной l ЭВМ, распространяющейся при ~токе со
скоростью света вдоль линии. Очевидно при частоте n=50 Гц l=![]() =
=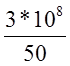 =6*106м
= 6000км. Для линий небольшой протяженности,
например, для линий расположенных в пределах города или района
это условие при стандартной частоте промышленного тока хорошо выполняется. В
сверхдальной линии (~1000км) между током в начале и в конце линии возникает
сдвиг фаз (~600), который
компенсируют специальными методами: естественно при таком сдвиге фаз
ток уже нельзя считать квазистационарным.
=6*106м
= 6000км. Для линий небольшой протяженности,
например, для линий расположенных в пределах города или района
это условие при стандартной частоте промышленного тока хорошо выполняется. В
сверхдальной линии (~1000км) между током в начале и в конце линии возникает
сдвиг фаз (~600), который
компенсируют специальными методами: естественно при таком сдвиге фаз
ток уже нельзя считать квазистационарным.
2.
Рассматриваемое поле не должно
охватывать больших участков V3, иначе говоря, точка наблюдения должна отстоять
от проводов с током на расстояниях, малых по сравнению с длиной волны
l. При
этом условии можно пренебречь тем запаздыванием, с которым
изменения поля следуют за изменениями тока, и условно
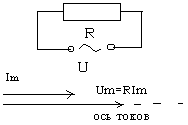
считать, что те и другие протекают одновременно (синхронно).Рассмотрим
сначала цепь переменного тока, содержащую только сопротивление R.
Пусть к зажимам сопротивления R (не обладающего индуктивностью и емкостью – такое
сопротивление называется активным) приложено напряжение, изменяющееся по
закону U=Umcos wt (Um – амплитудное
значение напряжения). При выполнении условия кваз-ти ток через сопротивление
определяется законом Ома : i = ![]() =
= ![]() coswt = Imcoswt. Таким образом, между
амплитудными значениями силы тока и напряжения имеется соотношение Im=
coswt = Imcoswt. Таким образом, между
амплитудными значениями силы тока и напряжения имеется соотношение Im=![]() . Изобразим это соотношение с помощью векторов (векторная
диаграмма). Выберем произвольное направление,
которое назовем осью токов. Отложим вдоль этого направления вектор тока длиной Im. Поскольку
напряжение и ток данном случае изменяются синфазно, вектор
напряжения также направлен вдоль оси токов. Мгновенная
мощность такой цепи: P(t) = i2R
. Для практики представляет интерес не мгновенное
значение мощности , а ее среднее значение
за период изменения тока: P =
. Изобразим это соотношение с помощью векторов (векторная
диаграмма). Выберем произвольное направление,
которое назовем осью токов. Отложим вдоль этого направления вектор тока длиной Im. Поскольку
напряжение и ток данном случае изменяются синфазно, вектор
напряжения также направлен вдоль оси токов. Мгновенная
мощность такой цепи: P(t) = i2R
. Для практики представляет интерес не мгновенное
значение мощности , а ее среднее значение
за период изменения тока: P =![]()
![]()
![]() 2Rdt
=
2Rdt
= ![]() Im2R. Величину I =
Im2R. Величину I = ![]()
![]() называют действующим значением силы переменного тока. (
также определяется и действующие значение напряжения). Действительное
значение силы тока ~ тока = силе постоянного тока, который в данной
цепи создает тепловой эффект, равный эффекту, создаваемому переменным током. Подадим ~
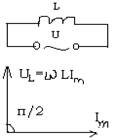
напряжение на концы индуктивности L с пренебрежимо малым
сопротивлением и емкостью. В индуктивности начнет течь переменный ток,
вследствие чего возникает ЭДС самоиндукции: Es = L
называют действующим значением силы переменного тока. (
также определяется и действующие значение напряжения). Действительное
значение силы тока ~ тока = силе постоянного тока, который в данной
цепи создает тепловой эффект, равный эффекту, создаваемому переменным током. Подадим ~
напряжение на концы индуктивности L с пренебрежимо малым
сопротивлением и емкостью. В индуктивности начнет течь переменный ток,
вследствие чего возникает ЭДС самоиндукции: Es = L![]() ( L не зависит от i). Уравнение
закона Ома: iR = (j1 - j2 ) + Е12
– запишется следующим образом ( R=0,
j1 -j2 = u , E12 = Es
): Umcos wt - L
( L не зависит от i). Уравнение
закона Ома: iR = (j1 - j2 ) + Е12
– запишется следующим образом ( R=0,
j1 -j2 = u , E12 = Es
): Umcos wt - L![]() = 0 или L
= 0 или L![]() = Umcoswt. В
рассматриваемом случае все внешнее напряжение приложено к индуктивности L
= Umcoswt. В
рассматриваемом случае все внешнее напряжение приложено к индуктивности L ![]() UL
= L
UL
= L![]()
![]() - падение напряжения на индуктивности.
Перепишем: L
- падение напряжения на индуктивности.
Перепишем: L ![]() di =
di = ![]() coswtdt. Интегрируя
получим i =
coswtdt. Интегрируя
получим i = ![]() sin wt + const. Постоянной
составляющей тока, очевидно нет, поэтому const = 0. Таким
образом, i= Im cos (wt -
sin wt + const. Постоянной
составляющей тока, очевидно нет, поэтому const = 0. Таким
образом, i= Im cos (wt - ![]() ), где Im
=
), где Im
= ![]() и роль сопротивления играет величина XL
=
и роль сопротивления играет величина XL
= ![]() - реактивное
индуктивное сопротивление. Учтя, что UL =
- реактивное
индуктивное сопротивление. Учтя, что UL = ![]() Um
coswt видим
, что падение напряжения на индуктивности опережает ток, текущий
через индуктивность, на
Um
coswt видим
, что падение напряжения на индуктивности опережает ток, текущий
через индуктивность, на ![]() .
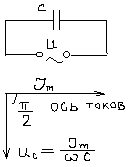
Пусть теперь напряжение подано на емкость С. Индуктивностью и
сопротивлением проводящих проводов будем пренебрегать. Емкость
непрерывно перезаряжается, вследствие чего в цепи течет ~
ток.Поскольку сопротивление проводящих проводящих проводов
пренебрежимо мало, напряжение на конденсаторе Uc =
.
Пусть теперь напряжение подано на емкость С. Индуктивностью и
сопротивлением проводящих проводов будем пренебрегать. Емкость
непрерывно перезаряжается, вследствие чего в цепи течет ~
ток.Поскольку сопротивление проводящих проводящих проводов
пренебрежимо мало, напряжение на конденсаторе Uc = ![]() можно считать = внешнему напряжению
U: Uc =
можно считать = внешнему напряжению
U: Uc = ![]() = Um coswt, i =
= Um coswt, i = ![]() = - wCUmsinwt = Im cos (wt +
= - wCUmsinwt = Im cos (wt + ![]() ),где Im
= wCUm. Величина Xc =
),где Im
= wCUm. Величина Xc = ![]() называют реактивным емкостным сопротивлением. Uc =
называют реактивным емкостным сопротивлением. Uc = ![]() Im coswt
Im coswt ![]() падение напряжения на
емкости отстает по фазе от текущего через емкость тока на
падение напряжения на
емкости отстает по фазе от текущего через емкость тока на ![]() . Мгновенное
значение мощности, выделяемой в цепи, = произведению
мгновенных значений напряжений и силы тока: P(t) = i(t) U(t) = Um coswt Im cos (wt - j ), используя
формулу cosa cosb =
. Мгновенное
значение мощности, выделяемой в цепи, = произведению
мгновенных значений напряжений и силы тока: P(t) = i(t) U(t) = Um coswt Im cos (wt - j ), используя
формулу cosa cosb = ![]() cos ( a +b) +
cos ( a +b) + ![]() cos ( a - b) получим P(t)
=
cos ( a - b) получим P(t)
= ![]() Um Im cosj +
Um Im cosj +![]() Um Im
cos(2 wt - j). Так как среднее
значение cos(2 wt - j) = 0, то среднее значение мощности P
Um Im
cos(2 wt - j). Так как среднее
значение cos(2 wt - j) = 0, то среднее значение мощности P![]() =
=![]() Um cosj. Или с использованием
действующих значений I =
Um cosj. Или с использованием
действующих значений I = ![]() и U =
и U = ![]() : P(t)
= I U cosj, где cosj - коэффициент мощности cosj =
: P(t)
= I U cosj, где cosj - коэффициент мощности cosj = ![]() =
= 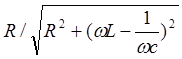 . Если
реактивное сопротивление X = wL -
. Если
реактивное сопротивление X = wL - ![]() = 0
= 0 ![]() cosj = 1 и P = UI.
При чисто реактивном сопротивлении цепи (R = 0 ) ,cosj = 0
cosj = 1 и P = UI.
При чисто реактивном сопротивлении цепи (R = 0 ) ,cosj = 0
![]() средняя
мощность, выделяемая в цепи = 0.
средняя
мощность, выделяемая в цепи = 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.