Метод наименьших квадратов (Лабораторная работа № 6), страница 2

№16	x	2.95	3.00	3.05	3.10	3.15	3.20
	y	6.610	7.081	7.553	8.047	8.561	9.084

№17	x	0.75	0.80	0.85	0.90	0.95	1.00
	y	2.768	2.833	2.903	2.979	3.062	3.153

№18	x	3,50	3,55	3,60	3,65	3,70	3,75
	y	37.140	36.850	36.010	34.430	34.210	33.130

№19	x	1.00	1.05	1.10	1.15	1.20	1.25
	y	1.000	0.974	0.651	0.523	0.818	1.206

№20	x	0.00	0.05	0.10	0.15	0.20	0.25
	y	-0.991	-0.480	-0.239	-0.103	-0.467	-0.886

№21	x	0.00	0.10	0.20	0.30	0.40	0.50
	y	0.000	0.144	0.311	0.490	0.659	0.711

№22	x	3.60	3.70	3.80	3.90	4.00	4.10
	y	1.279	1.300	1.340	1.363	1.391	1.413

№23	x	5.05	5.15	5.25	5.35	5.45	5.55
	y	-11.500	-12.285	-13.101	-13.959	-14.831	-15.744

№24	x	0.10	0.20	0.30	0.40	0.50	0.60
	y	0.911	0.521	0.382	0.111	0.283	0.671

№25	x	0.50	0.60	0.70	0.80	0.90	1.00
	y	0.421	1.671	2.824	3.061	1.912	0.344

№26	x	1.80	2.00	2.20	2.40	2.60	2.80
	y	3.482	3.504	3.701	4.003	4.151	4.208

№27	x	1.80	2.00	2.20	2.40	2.60	2.80
	y	5.211	6.250	7.404	8.878	10.077	11.604

№28	x	1.00	1.10	1.20	1.30	1.40	1.50
	y	2.382	2.362	2.343	2.324	2.306	2.289

№29	x	0.00	0.20	0.40	0.60	0.80	1.00
	y	-1.348	-0.634	-2.200	0.000	-1.406	-0.920

№30	x	1.10	1.30	1.50	1.70	1.90	2.10
	y	2.284	3.155	0.271	2.677	3.690	1.937

ЛАБОРАТОРНАЯ РАБОТА №6

«Метод наименьших квадратов»

Задание. Методом наименьших квадратов для данной зависимости найти приближающую функцию.

По заданной таблице значений функции построить точечный график функции и выдвинуть гипотезы о виде приближающей функции.
Составить две приближающих функции в соответствии с выдвинутыми гипотезами:

2.1. Если это необходимо по исходной таблице составить новую таблицу, для использования приближающей функции линейного вида.

2.2. Провести расчет коэффициентов используя таблицу:

2.3. Вычислить параметры а и в:

а = (M_xy - М_х М_y)/(-( М_х)²); в = М_y - М_х*(M_xy - М_х М_y)/(-( М_х)²)

(если приближающая функция содержит три параметра, то найти их решая систему уравнений )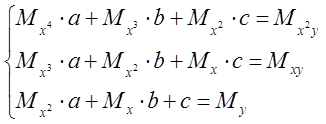

3.1. Составить таблицу:

3.2. Сравнить σ₁ и σ₂.

1 2

Σ