Изучение электростатического поля: Методическое пособие к лабораторной работе № 2, страница 2

Условились при изобра-жении электрических по-лей с помощью линий напряжённости, число силовых линий, проходящих через единичную поверхность, перпендикуляр-ную к силовым линиям в данной точке поля, выбирать рав-ным напряжённости поля  Е в данной точке (в этом состоит правило графического изображения полей с помощью силовых линий). При таком условии картина силовых линий электрического поля позволяет наглядно судить как о направлении, так и о величине напряжённости поля в каждой точке.

§3. Потенциал

электрического поля

Помимо напряжённости электрическое поле характеризуется ещё одной важной физической величиной – потенциалом.

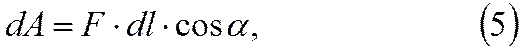Рассмотрим перемещение заряда  q в поле другого точечного заряда  q₀ из точки  1  в точку  2 (см. РИС.3). Работа силы  F на элементарном перемещении  dl определяется соотношением

 

но                          зна-чит  dA = Fdr . Подста-вим сюда вместо силы её значение из закона Кулона, получим :

 

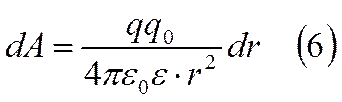Для вычисления работы перемещения заряда из точки  1  в точку  2  по произвольному пути 1-2 проинтегрируем (6) в пределах от  r₁  до  r₂ , получим

 

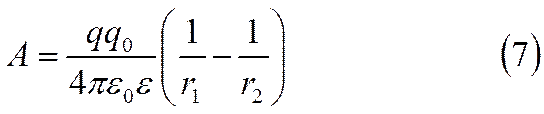Из выражения (7) следует, что работа перемещения электри-ческого заряда не зависит от формы пути, по которому перемещается заряд, а зависит только от начальной и конечной  точек. Если заряд  q , перемещаясь в электрическом поле, возвращается в исходную точку (r₂ = r₁), то работа перемещения заряда по замкнутому пути в электростатическом поле равна нулю. Поля, обладающие указанным свойством, называются потенциальными.

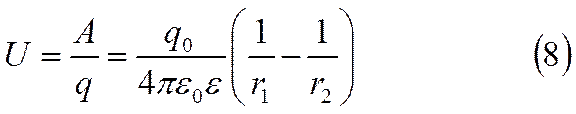Найдём отношение работы перемещения заряда к величине этого заряда :

Эта величина не зависит от величины перемещаемого заряда и от пути, по которому он перемещается, и поэтому служит характе-ристикой поля, созданного зарядом  q₀ , и называется разностью потенциалов или электрическим напряжением.

Разность потенциалов двух точек  1  и  2  электрического поля измеряется работой, совершаемой полем при перемещении единичного положительного заряда между этими точками.

Следует подчеркнуть, что разность потенциалов имеет смысл характеристики поля потому, что работа перемещения заряда не зависит от формы пути. Действительно, если бы работа переме-щения заряда зависела от пути, то при перемещении одного и то-го же заряда между теми же самыми точками поля, это отношение  A /q  не являлось бы однозначной характеристикой этих точек поля.

Если выбрать какую-либо точку пространства в качестве на-чальной точки (точки отсчёта), то любой точке можно сопоставить разность потенциалов относительно этой начальной точки.

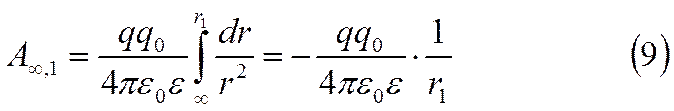Для случая поля точечного заряда наиболее простое матема-тическое выражение для потенциала получается, если в качестве начальной выбрать любую точку, удалённую на бесконечность. Тогда работа перемещения положительного заряда  qиз беско-нечности в данную точку поля, созданного другим точечным за-рядом  q₀ , будет равна

Отношение работы перемещения положительного заряда из бесконечности в данную точку поля к величине этого заряда (работа по перемещению единичного заряда) называется потенциалом данной точки поля :

 

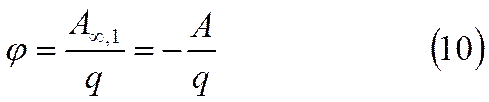Знак минус в этом выражении означает, что в данном случае работа совершается внешними силами против сил поля.

Очевидно, что напряжение  U  между произвольными точка-ми  1  и  2  электрического поля и потенциалы этих точек    связаны простым соотношением

Для поля точечного заряда

 

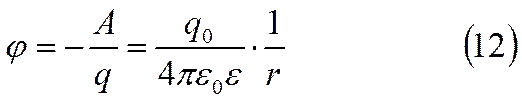
Потенциал любой точки поля, созданного положительным за-рядом – положителен и убывает до нуля по мере удаления от за-ряда. Напротив – потенциал поля, созданного отрицательным за-рядом, - отрицательная величина и растёт до нуля по мере удале-ния от заряда.

Из выражения для потенциала (12) следует, что потенциал любой точки сферической поверхности  S  c центром в точке расположения заряда одинаков (см. РИС.4). Такие поверхности называются поверхностями равного потенциала  или  эквипо-тенциальными поверхностями.  

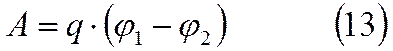Работу перемещения заряда можно выразить через разность потенциалов

Отсюда следует, что работа пере-мещения заряда по эквипотенци-альной поверхности равна нулю. Это значит, что сила, действую-щая на заряд, а следовательно, и вектор напряжённости поля  Е  направлены перпендикулярно эк-випотенциальной поверхности.

Используя эквипотенциаль-ные поверхности, можно также дать графическое изображение электрического поля.