Закон сохранения механической энергии

4

Закон сохранения механической энергии можно сформулировать следующим образом: механическая энергия сохраняется в процессе  движения замкнутых механических систем и систем, находящихся в стационарных потенциальных силовых полях; указанный закон является следствием  однородности времени.

Действительно для любой механической системы, относящихся к одному  из двух  указанных классов, можно ввести понятие о полной потенциальной энергии. У замкнутых систем  она состоит из внутренней потенциальной энергии  парного взаимодействия частиц.

           (1)       

Вследствие однородности  времени (физ., эквивалентности различных его моментов по отношению к замкнутой системе) потенциальная энергия (1) не может быть явной функцией времени t. Полная потенциальная энергия системы, находящейся в стационарном  потенциальном  поле, складывается из ее внутренней части U⁽ⁱ⁾ и внешней части U^(e) , описывающей взаимодействие системы с внешним силовым магнитным полем. Но так как внешнее поле стационарно, то полная потенциальная энергия такой системы является явной функцией времени t, т.е.

                  (2)

Из выражения (1) и (2) видно, что полную производную по времени  от потенциальной энергии  как замкнутой системы, так и системы, находящейся в стационарном  потенциальном силовом поле  можно записать в виде

                                                              (3)

Заметим, что если бы время  не обладало свойством однородности  (т.е. можно было бы опытным путем установить физическую неравноценность различных моментов времени), то это неизбежно привело бы  к явной зависимости от временной потенциальной энергии  любой из рассматриваемых нами систем, при этом в полную производную (3),  пришлось бы дополнительно включить частную производную.   

Обратимся теперь к системе дифференциальных уравнений движения, которую, имея в виду потенциальный характер  всех внешних  и внутренних сил, действующих на механические системы, мы запишем в виде    (4)  умножая i- тое уравнение системы (4)    скалярно на вектор  и учитывая очевидное равенство:

                                     (5)

Получим новую систему уравнений

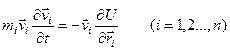,                                (6)

Равносильную  системе (4). Складывая почленно  уравнения (6) и изменяя в левой части  получаемого при этом равенства  порядок выполнения операций суммирования и дифференцирования, получаем уравнение

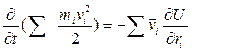                                 (7)

которое, используя выражение (3), можно окончательно записать в виде

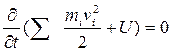                                               (8)

уравнение (8) показывает, что в процессе движения  у замкнутой  механической системы, находящейся в стационарном потенциальном  поле, сохраняется скалярная величина 

 

Сохраняющуюся величину Е называют полной механической энергией системы: она складывается из двух существенно различных членов: кинетической энергии

 

зависящей от скоростей частиц, и потенциальной энергии U, зависящей  от их координат E=T+U=const. Нетрудно видеть, что полная энергия обладает  свойством аддетивности: если пренебречь взаимодействием частиц, то полную энергию замкнутой системы и системы находящейся  в потенциальном силовом поле, можно представить в виде

 

где E_i – полная механическая энергия  отдельной частицы. Механической системы, у которой  полная энергия сохраняется, принято называть  консервативными. Закон сохранения для  консервативной  системы происходит в непрерывном превращении ее кинетической энергии  в потенциальную и обратно. В этом состоянии закон сохранения (9) является частным случаем всеобщего закона сохранения и превращения энергии различных форм движения материи.

Для механических систем, находящихся не в стационарных силовых полях  тоже можно ввести понятие о полной потенциальной энергии  как суммы потенциальных энергий системы во внешнем силовом поле, явно зависящем от времени, и энергии взаимодействия частиц, входящих в систему.

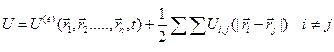       (14)

чтобы получить эту теорему, продифференцируем  выражение  (10) для кинетической энергии системы  по времени:

                     (15)

Учитывая не потенциальный характер действующих на систему  сил, запишем дифференциальное, уравнение движения системы

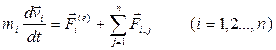                     (16)

подставляя (16) в (15), получаем дифференциальную формулировку теоремы об изменении кинетической энергии:

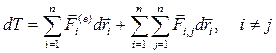   (17)

Т.о., полный дифференциал кинетической энергии системы равна сумме элементарных работ всех внешних и внутренних сил, действующих на частицы системы.