Трехфазные цепи. Определение линейных токов приемников; тока в нейтральном проводе; активную мощность всей нагрузки, страница 3

Пример расчета.

Исходные данные:

Uл, В	приемники соединения «звезда»			приемники соединения «треугольник»
	Z 1a, Ом	Z 1b, Ом	Z 1c, Ом	Z 2a, Ом	Z 2b, Ом	Z 2c, Ом
220	8 + j 20	8 – j 25	15	18 + j 6	5	14 -  j 16

                             N    A  B C 

 

            Z 1a                                                     Z 2a

 

                                    a            I_a2                                  I_ab  

 I_N                  I_a1                                                                                                                                        

              Z 1b                                                   Z 2b      

 

                                         b

                Z 1       I_b1                 I_b2               Z 2c                I_bc                  

 

                                             c

                   I_c1                            I_c2                                        I_ca

Рисунок 1.2

Решение:

1)  соединение приемников «звезда»

по условию задано U_л = 220 В, так как генератор вырабатывает симметричную систему напряжений, то фазные напряжения можно записать в следующем виде:

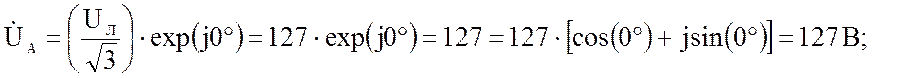
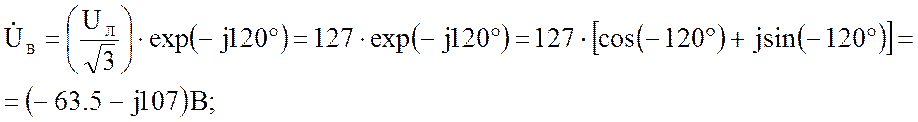
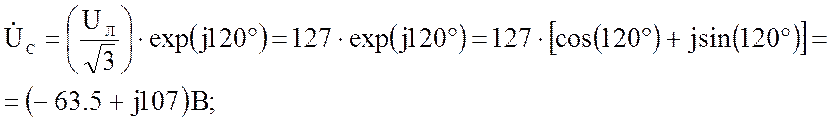
Запишем фазные сопротивления в показательной форме:

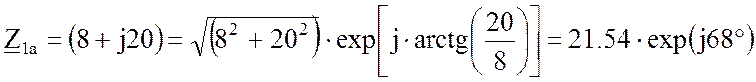, Ом;

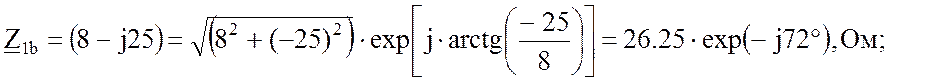
, Ом, где

φ_1a = 68˚, φ_1b = -72˚, φ_1c = 0˚.

В соединении «звезда» фазные токи равны линейным токам, следовательно, определяем линейные токи приемников (по закону Ома для участка цепи) и ток в нейтральном проводе (по I-му закону Кирхгофа для узла):

;

.

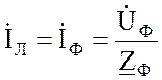_Aå, А;

_Bå, А;

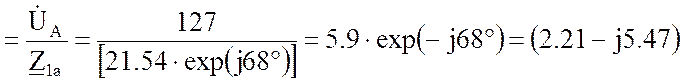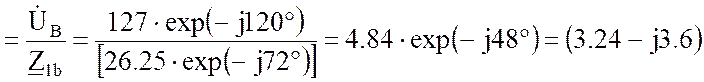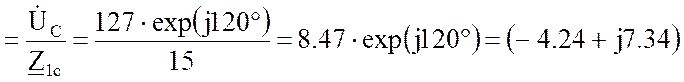_Cå, А.

 = 2.21 –j5.47 +3.24 –j3.6 – 4.24 + j7.34  = 1.21 –j1.73 =

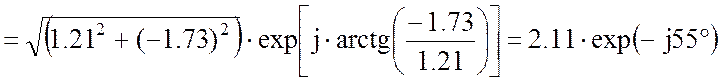, A.

Определяем активную мощность приемников, соединенных «звездой».

Активная мощность фазы определяется по формуле: P_ф =  U_ф·I_ф·cos(φ_ф), следовательно,

P_Aå = U_A· I_A·cos(φ_A)  = 127·5.9·cos(68˚) = 280.69, Вт;

P_Bå = U_B· I_B·cos(φ_B)  = 127·4.84·cos(-72˚) = 189.95, Вт;

P_Cå = U_C· I_C·cos(φ_C)  = 127·8.47·cos(0˚) = 1075.69, Вт.

2)  соединение «треугольник»

для данного соединения линейные напряжения соответствуют фазным, а фазные токи отличаются от линейных.

Определим фазные напряжения:

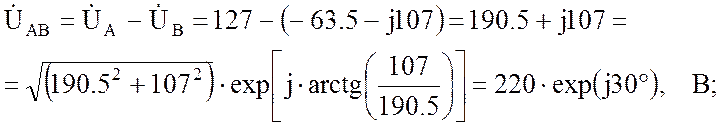
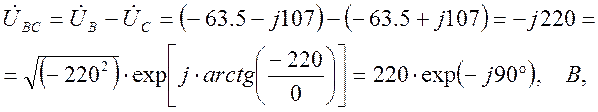
то есть вектор этого напряжения совпадает с осью мнимых значений комплексной плоскости;

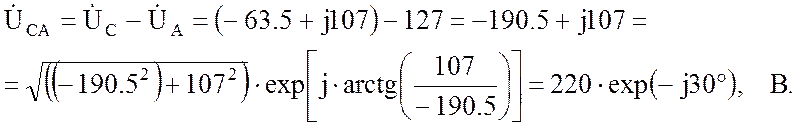
Запишем фазные сопротивления в показательной форме:

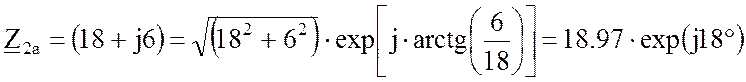, Ом;

, Ом;

 

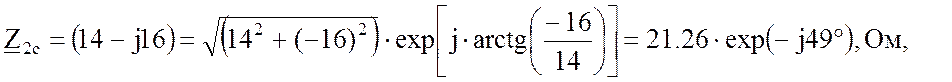
где

φ_2a = 18˚, φ_2b = 0˚, φ_1c = -49˚.

Определяем фазные токи приемников (по закону Ома для участка цепи), соединенных «треугольником»:

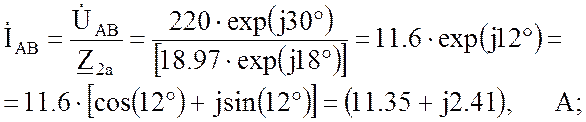
_BC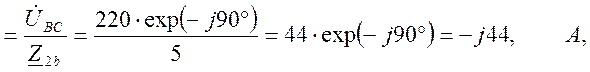 

так как ток данной фазы совпадает с напряжением (нагрузка данной фазы чисто активная);

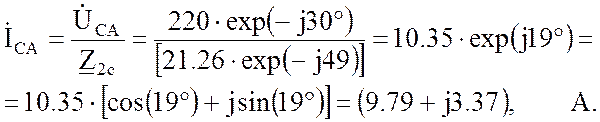
Определяем линейные токи приемников (по I-му закону Кирхгофа для узла), соединенных «треугольником»: