2.
Время работы изделия до отказа
подчиняется закону распределения Релея (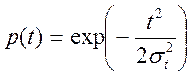 ). Требуется вычислить количественные характеристики
надежности изделия p(t), f(t), λ(t), mt для t=150час, если параметр
распределения σt=100 час. Показать на графиках изменение p(t),
f(t), λ(t), mt.
). Требуется вычислить количественные характеристики
надежности изделия p(t), f(t), λ(t), mt для t=150час, если параметр
распределения σt=100 час. Показать на графиках изменение p(t),
f(t), λ(t), mt.
|
Дано: |
Решение: |
|
t=150час σt=100 час |
1. Вычислим вероятность безотказной работы p(t)
2. Определим частоту отказа f(t) f(t)=tp(t)/ σ t2 ; f(100)=10000.325/1502=0.44 (1/час). 3. Рассчитаем интенсивность отказов λ(t)= t/ σ t 2 ; λ (100)=150/1002 =0,015 1/час. 4. Определим среднее время безотказной работы изделия:
|
3. Задача. Дана система из трёх последовательно соединённых элемента. Имеет место нормальный закон распределения времени работы до отказа:
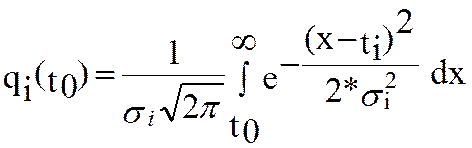
с параметрами T1=100ч. , s1=10ч.;T2=150ч., s2 = 15ч.; T3=100ч. , s3 = 20ч.
Требуется вычислить количественные характеристики надежности ситемы p(t), f(t), λ(t), mt для t=1500час,
|
Дано: |
Решение: |
|
T1=100ч. , s1=10ч.; T2=150ч., s2 = 15ч.; T3=100ч. , s3 = 20ч |
1. Вычислим вероятность безотказной работы p(t) каждого элемента λ1=1/100=0,01 λ2=1/150=0,06 λ1=1/100=0,01 P1(t)=0,36 P2(t)=0,02 P3(t)=0,36 2. Найдем вероятность безотказной работы системы: Рс=Р1*Р2*Р3 =0,00032 3. Определим частоту отказа f(t) fc(t) = λ ce- λc*t = λc *Pc(t)=0,026*0,00032=8,32*10-6(1/час) 4. Рассчитаем интенсивность отказов Здесь λ i - интенсивность отказов i -го блока. Здесь λ c - интенсивность отказов системы. 5. Определим среднее время безотказной работы изделия: |
7. Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ 1=0,16*10-3 (1/час) (т.е. const). Интенсивности отказов двух устройств зависят от времени и определяются следующими формулами: λ2=0,2*10-4t (1/час),
λ 3=0,01*10-6t2 (1/час).Необходимо рассчитать вероятность безотказной работы изделия в течение 100 час.
|
Дано: |
Решение: |
|
λ 1=0,16*10-3 (1/час) λ2=0,2*10-4t (1/час) λ 3=0,01*10-6t (1/час) t=100ч |
Решение. На основании формулы (3.3) имеем
Для t=100 час
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.