Исследование объекта и разработка системы управления процессом вулканизации автомобильных покрышек, страница 2

 

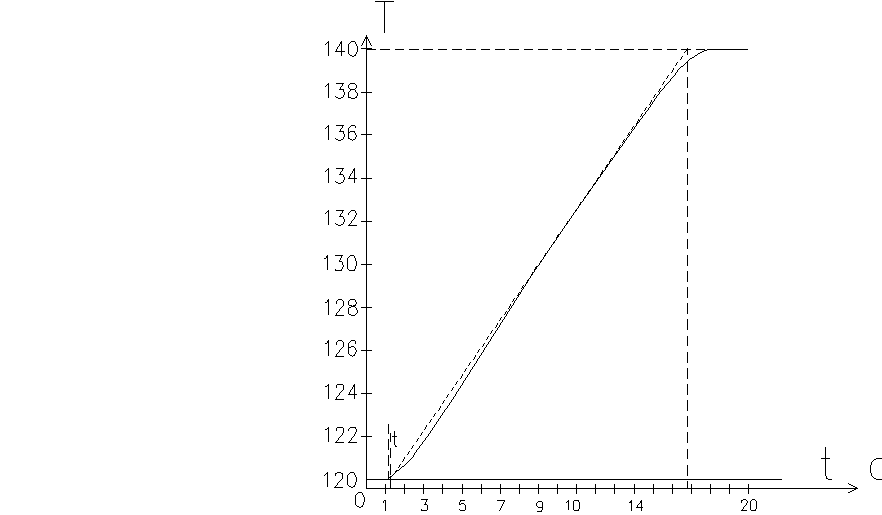
                                                 Рисунок 2.1-Кривая разгона

В расчёте использовались следующие данные: Т = 16; = 16; К = 1; m = 0,221. По расчётным данным строим тарированные кривые разгона, то есть, проверяем, отражает ли выбранное дифференциальное уравнение кривой разгона. Экспериментальная тарированная кривая, не должна превышать 20 % от теоретической, если выполняется это условие, то снятая кривая разгона может получиться из дифференциального уравнения, путём использования преобразования по Лапласу.

;                                                                 (2.1)

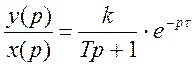;                                                                             (2.2)

По тарированной кривой разгона делаем вывод, что данный объект описывается дифференциальным уравнением первого порядка, то есть дифференциальное уравнение, адекватно процессу и дифференциальное уравнение выбрано правильно.

По кривой разгона получено время запаздывания τ = 16сек.

Тогда передаточная функция звена чистого запаздывания объекта:

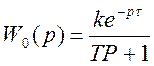      ;                                                                                   (2.3)

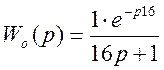;                                                                                  (2.4)

Для получения частотной характеристики объекта, заменим , получаем

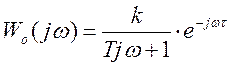;                                                                          (2.5)

После преобразований получим

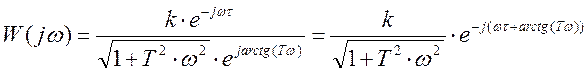;                                     (2.6)

Из данной формулы АЧХ и ФЧХ:

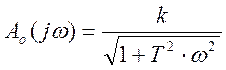;                                                                                  (2.7)

;                                                                        (2.8)

По двум последним формулам производим расчёты и сводим их в таблицу 2.1и 2.2

             Таблица 2.1- Амплитудно-фазо-частотные характеристики

			ωτ
0	0	1	0	0	0
0,02	0,32	0,907	0,32	17,744	-36,08
0,04	0,64	0,842	0,64	32,619	-69,291
0,06	0,96	0,721	0,96	43,830	-98,838
0,08	1,28	0,615	1,28	52,0	-125,34
0,1	1,6	0,529	1,6	57,9	-149,55
0,15	2,4	0,384	2,4	67,38	-204,94
0,2	3,2	0,298	3,2	72,64	-255,04
0.25	4	0,242	4	75,96	-303,96
0,3	4,8	0,203	4,8	78,23	-351,83
0,35	5,6	0,175	5,6	79,87	-399,07
0,4	6,4	0,154	6,4	81,11	-445,9

По передаточной функции получаем расширенную амплитудно-фазо-частотную характеристику, чтобы (критерий Найквиста), а также сдвиг по фазе был . Это определяем для расчёта регулятора. Необходимо подобрать амплитудо-фазо-частотную характеристику, чтобы переходный процесс затухал. Эта характеристика показывает, на сколько меняется амплитуда и фаза. Необходимо чтобы произведение модулей .

           Таблица 2.2- Динамические характеристики объекта