Явление радиоактивности, виды радиоактивности. Классификация элементарных частиц (кварки). Альфа-распад ядер и его особенности. Кварковая структура адронов. Счетчики Гейгера-Мюллера. Прохождение гамма-квантов через вещество, страница 4

1)для простых одіночн. распадов это линейн.зависимость, т.е. отклонение (*) не происх. 2) отклонен. от экспоненц. з-на возожн. если: а)в реакциях присуств. не 1 , а 2 или более сорта радиоакт. ядер. б) набл. цепочка последовательн. распадов одного и того же ядра.1®2®3. получили з-н по кот. происх. цепочка распадов рассм. 3 сл.: 1) 1-е ядро короткоживущее,2-е ядро-долгоживущее l₁>>l₂, коэф прі экспоненте будет иметь одинаков знаки, значит кривая lna не б/т иметь перегибов.2) 2-е ядро короткоживущее, 1-е ядро-долгоживущее l₁<l₂ , коэф при 2-й экспоненте будет иметь отриц., показатли ее степени по модулю превыш. граф. немонотонной,а имеет мах. вначале происх. увелич.за счет накоплений ядер 2. потом если t мало по сравнению с t₁, то соотнош. м/у ядрами 1 и 2 становятся независ. от вр., т.е. набл. радиоакт. равновесие. Затем уменш. числа ядер N₁ и N₂ со скоростью распада ядра 1. 3) Пусть l₁<<l₂, тогда Т_1/2¹ первого эл-та >> Т_1/2 последуюш. эл-тов. Ч/з вр. t>>Т_1/2² устанавл. вековое равновесіе, прі кот. кол-во ядер кажд. изотопа ~Т_1/2 этого изотопа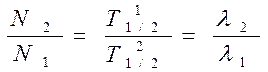
Билет №5

Релятивистские и квантовые св-ва частиц.

№1. Релятивистские св-ва частиц

Релятив. св-ва проявл-ся для больших скоростей и высоких энергий.

Для покоящихся частиц:  (1).где т – масса покоя.

Для движ-ся частицы:  (2), если т=0, то  (3).

Условие малости релятивст. Эффектов  .

№2 Квантово-механические св-ва частиц.

Чем меньше частица и расстояние м/у частицами, тем ярче проявл-ся квантовые св-ва. Фундаментальной квантовой постоянной явл. пост. Планка.

;

1.  Корпускулярно волновой дуализм. Для частицы с энергией Eи импульсом  справедливы: 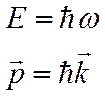} (4), где  - круговая частота, кот. равна .  - направление распространения волны 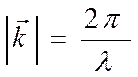, - длина волны.

2.  Соотношение неопределенности Гейзинберга. Они устанавливают количественные пределы применимости классических понятий коор-ты и импульса, времени и энергии.

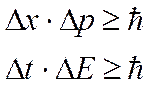} (5) где  неопр-ть значения коор-ты, 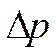 - неопр-ть значения импульса.

№3.Формальное положение квантовой механики.

1.  Состояние системы в кв. мех-ке задается волновой ф-ей:  - комплексн.

2.  Ур-ние движ-я частицы – это ур-ние Шредингера:,  - оператор Гомельтона.

3.  Каждой физ. величине в кв. мех-ке ставится в соответствие линейный оператор, действующий на волновую ф-ю: , .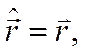

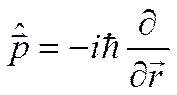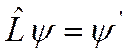№4 Среднее значения оператора.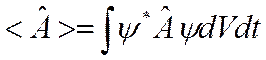

№5 Физ. смысл волновой функции . 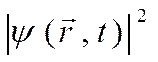задает плотность вер-ти найти частицу в момент времени t в коор-те .

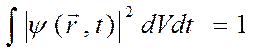 - условие нормировки.

Мультипликативные законы сохранения в реакциях элементарных частиц.

Величина	Взаимодействие
	Сильное	Эл/м	Слабое	Гравит.
Мультипликативные
1) Пространственная четность P**	+	+	-	+
2) Зарядовая четность С***	+	+	-	+
3) Временная четность Т****	+	+	+	+
4) Комбинированная четность СР	+	+	-	+
5) СРТ теорема (четность)*****	+	+	+	+

* - нарушение законов сохранения квантовых чисел кварков в слабом взаимодействии говорит о том, что реакция идет за счет слабого взаимодействия.

** - операция пространственной четности приводит к замене пространственных координат на противоположные

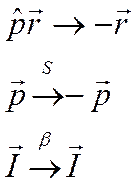
Билет №6

Электрический и барионный заряд ядер. Дорожка стабильности ядер. Радиус и плотность ядер.

С числами А и z тесно связана зарядовая хар-ка ядра, эл. заряд ядра, кот. равен 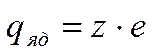. Эл. заряд – величина целочисленная и сохран. при  взоимод-ях. В 1938 г. Для объяснения стабильности протона был введенный барионный заряд. Согласно з-нам сохр-я момента импульса, энергии, эл. заряда распад протона на более мелкие частицы возможен. А согласно з-ну сохрон. барионного заряда – невозможен. Барионный заряд обеспечивает стабильность атомных ядер.