



ЛАБОРАТОРНАЯ РАБОТА
ПРОВЕРКА ЗАКОНА БУГЕРА-ЛАМБЕРТА-БЕРА
Цель работы:Зарегистрировать спектры поглощения ряда растворов и оценить, в какой степени к этим растворам применим закон Бугера-Ламберта-Бера.
Приборы: Cпектрофотометр СФ-46, набор кювет.
Закон ослабления монохроматического (с длиной волны λ) излучения при поглощении его слоем однородного вещества выражается в виде (закон Бугера-Ламберта-Бера):
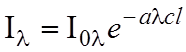 ,
(1)
,
(1)
или
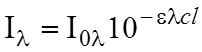 ,
(2)
,
(2)
где
![]() - интенсивность излучения, падающего на
вещество;
- интенсивность излучения, падающего на
вещество;
![]() - интенсивность излучения, прошедшего
через слой вещества, толщиной l;
- интенсивность излучения, прошедшего
через слой вещества, толщиной l;
с – концентрация вещества;
аλ – показатель поглощения;
![]() =0,434аλ – коэффициент
экстинкции.
=0,434аλ – коэффициент
экстинкции.
В логарифмической форме закон ослабления (2) имеет вид:
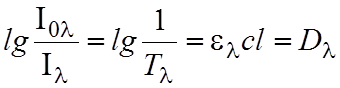 (3)
(3)
где
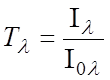 - коэффициент пропускания;
- коэффициент пропускания;
![]() - оптическая плотность.
- оптическая плотность.
Зависимость
оптической плотности ![]()
![]() или коэффициента экстинкции ελ (λ), εν (ν) называется спектром поглощения.
или коэффициента экстинкции ελ (λ), εν (ν) называется спектром поглощения.
Закон Бугера, строго говоря, справедлив лишь для проходящего через гомогенную изотропную среду плоскопараллельного пучка монохроматического света при соответствии величины С в уравнениях (1) – (3) истинной концентрации вещества в растворе и незначительной заселенности возбужденных энергетических уровней. Если толщина слоя lвыдерживается постоянной, то зависимость D = D (C) изображается прямой линией, проходящей через начало координат с тангенсом угла наклона.
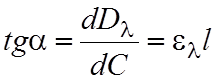
Нарушение указанных условий
приводит к кажущимся отклонениям от закона Бугера, выражающимся в искривлении
зависимости D(с), т.е. коэффициент экстинкции ![]() перестает быть постоянным с ростом
концентрации С.
перестает быть постоянным с ростом
концентрации С.
Наиболее часто встречающиеся отклонения от закона Бугера можно разделить на две группы:
1)
Физико-химические причины. К ним относится, прежде всего,
несоответствие подставляемой в уравнение Бугера концентрации вещества в
растворе. Это несоответствие может быть вызвано реакциями диссоциации,
ассоциации или химического взаимодействия растворенного вещества с
растворителем (если коэффициенты экстинкции продуктов этих реакций отличаются
от коэффициентов экстинкции исходных веществ). Если константы этих процессов и
коэффициенты экстинкции продуктов известны, то отклонения от закона Бугера
могут быть устранены подстановкой в (3) истинных значений С и ![]()
![]() .
Часто удается подобрать интервал концентраций, в котором явления ассоциации и
диссоциации не наблюдаются и отклонения от закона Бугера отсутствуют.
.
Часто удается подобрать интервал концентраций, в котором явления ассоциации и
диссоциации не наблюдаются и отклонения от закона Бугера отсутствуют.
Другой физико-химической причиной отклонения от закона Бугера является флуоресценция анализируемого вещества. Попадание флуоресцентного излучения на фотоэлемент приводит к увеличению выходного сигнала, что, естественно, снижает экспериментально определяемую оптическую плотность. Вследствие частичной реабсорбции флуоресцентного излучения наблюдаемые отклонения будут зависеть от толщины кюветы.
Кроме того, отклонения от закона Бугера могут проявляться из-за неравномерного распределения поглощающего вещества в пучке света (в кювете).
Пропорциональность зависимости нарушается также при чрезвычайно большой интенсивности падающего на вещество излучения (лазерная электроскопия), когда значительная часть молекул вещества оказывается в возбужденных состояниях, и заселенность основного состояния, с которого происходят абсорбционные переходы, не соответствует концентрации вещества в растворе.
2) Инструментальные причины. Очевидной инструментальной причиной отклонений от закона Бугера может быть нелинейная зависимость показаний прибора от интенсивности излучения (нелинейная энергетическая характеристика приемника излучения).
Наиболее частой инструментальной причиной
кажущихся отклонений от закона Бугера является немонохроматичность падающего на
образец излучения. В общем случае увеличение ширины щели спектрального прибора h, а следовательно, и спектрального интервала, выделяемого
при этом S=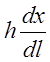 , приводит к уменьшению
измеряемых в области максимумом полос значений D и
, приводит к уменьшению
измеряемых в области максимумом полос значений D и ![]() . Для того, чтобы избежать этих отклонений,
необходимо, чтобы спектральная ширина щели S была
меньше полуширины исследуемой полосы
. Для того, чтобы избежать этих отклонений,
необходимо, чтобы спектральная ширина щели S была
меньше полуширины исследуемой полосы ![]() .
.
Помимо конечной ширины щели, немонохроматичность излучения может быть вызвана присутствием рассеянного света. К рассеянию света приводят, например, дефекты в призмах, зеркалах и дифракционных решетках, пыль на оптических деталях и т.п. длины волн рассеянного излучения не ограничены каким-либо интервалом, и интенсивность рассеянного излучения мало зависит от длины волн.
Уровень рассеянного излучения характеризуют величиной:
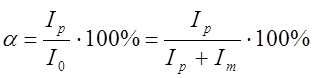 , (4)
, (4)
где Ip и Im – интенсивность рассеянного и монохроматического (полезного) излучения.
Так как Ip мало зависит от длины волны, величина ![]() особенно велика в тех областях спектра,
где мала интенсивность источника излучения, т.е. мало Im.
Это особенно характерно для дальней УФ-области (190-220нм).
особенно велика в тех областях спектра,
где мала интенсивность источника излучения, т.е. мало Im.
Это особенно характерно для дальней УФ-области (190-220нм).
В присутствии рассеянного излучения измеряемое значение коэффициента пропускания равно
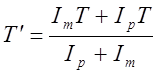 ,
(5)
,
(5)
где Т и Тр – коэффициент пропускания монохроматического и рассеянного излучения.
Из (4) и (5) следует выражение для погрешности, вносимой в измерение коэффициента пропускания вследствие рассеяния:
![]() (6)
(6)
Анализ уравнения (6) показывает, что с
уменьшением Т (увеличением D) погрешность ![]() возрастает. При Тр<Т
рассеянный свет приводит к уменьшению, а при Тр>Т – к увеличению
измеряемого значения коэффициента пропускания по сравнению с истинным.
возрастает. При Тр<Т
рассеянный свет приводит к уменьшению, а при Тр>Т – к увеличению
измеряемого значения коэффициента пропускания по сравнению с истинным.
Порядок выполнения работы
1. Подготовить серию водных стандартных растворов окрашенного соединения (концентрация ~ 10-4 моль/л).
2. Зарегистрировать спектр поглощения одного из них в области (300-1000) нм.
3.
Определить ![]() - длину волны, соответствующую
максимальному значению оптической плотности (
- длину волны, соответствующую
максимальному значению оптической плотности (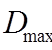 ).
).
4. Измерить
оптическую плотность ![]() для всех растворов при заданной
толщине кювет и построить график зависимости
для всех растворов при заданной
толщине кювет и построить график зависимости  =f(c).
=f(c).
5. Измерить
оптическую плотность для каждого раствора, используя кюветы различной толщины.
Построить график зависимости ![]() =f(l).
=f(l).
6. Сделать вывод о наличии или отсутствии отклонений от закона Бугера-Ламберта-Бера.
7. Графически определить коэффициент экстинкции анализируемого вещества.
8. Рассчитать
среднеквадратичную ошибку в измерении ![]() по
формуле:
по
формуле:
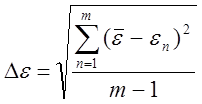 ,
,
где ![]() -
среднее значение коэффициента экстинкции;
-
среднее значение коэффициента экстинкции;
m – число измерений.
Примечание. Измерение оптической плотности растворов проводить относительно растворителя, т.е. в канал сравнения помещать кювету с водой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.