



ЛАБОРАТОРНАЯ РАБОТА
ОПРЕДЕЛЕНИЕ СИММЕТРИИ МОЛЕКУЛ ИЗ АНАЛИЗА ИХ КОЛЕБАТЕЛЬНЫХ СПЕКТРОВ
Цель работы: Изучение свойств симметрии колебаний многоатомных молекул. Определение группы симметрии молекулы XY3 на основе ее колебательных ИК и КР спектров.
Задание
1. Проанализировать возможные структурные модификации молекулы XY3 и соответствующие им точечные группы симметрии.
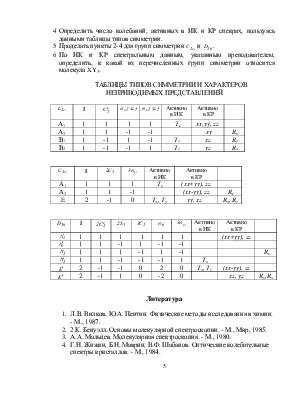
2. Определить число нормальных колебаний и их активность для ИК и КР спектров в случае каждой возможной структурной модификации молекулы XY3
3. Определить на основе ИК и КР колебательных спектров, к какой структурной модификации относится молекула XY3 .
4. Изучить следующие вопросы:
· Классификация колебаний многоатомных молекул.
· Основные понятия теории групп, используемые при описании молекулярных колебаний.
· Типы симметрии молекулярных колебаний.
· Активность нормальных колебаний в ИК и КР спектрах.
При анализе нормальных колебаний многоатомных молекул важное значение имеет их симметрия, которая определяется свойствами симметрии равновесной ядерной конфигурации молекулы. Учет этих свойств, с одной стороны. Облегчает расчет колебательных спектров, так как позволяет проводить разделение колебательной задачи. С другой стороны, симметрия нормальных колебаний определяет их активность (правила отбора) в ИК и КР спектрах, и сопоставление этих экспериментально наблюдаемых спектров позволяет определить симметрию молекулы.
Под симметрией молекулы понимается вся совокупность имеющихся у него элементов симметрии. Элементам симметрии соответствуют операции симметрии, переводящие молекулу саму в себя. Возможные комбинации операций симметрии, оставляющих без изменения хотя бы одну точку, называются точечными группами симметрии. Существуют следующие элементы (операции) симметрии:
1. Сn– поворотная ось симметрии порядка n; соответствующая ей операция симметрии – поворот на угол p= 2π/n, где p принимает значения от 1 до n – 1.
2. σ – плоскость симметрии; соответствующая ей операция симметрии – отражение в плоскости.
3. i – центр симметрии; операция симметрии – инверсия (отражение) в точке.
4. Sn – зеркально-поворотная ось симметрии порядка n; операция симметрии – поворот на угол p= 2π/n с одновременным отражением в плоскости, перпендикулярной оси.
5. I (или C1) – вводимый для общности тождественный элемент симметрии; соответствующая операция симметрии – операция идентичности или тождественного преобразования – оставляет молекулу в покое.
Любая молекула относится к какой-то точечной группе симметрии, если не исключать и тривиальную группу С1, не имеющую элементов симметрии, кроме тождественного преобразования.
Полные совокупности операций симметрии точечных групп даны в таблицах типов симметрии и характеров представлений.
При колебаниях молекулы возможны только определенные комбинации свойств симметрии смещенной ( от равновесной) ядерной конфигурации, если иметь в виду ее отношение к операциям симметрии точечной группы. Эти комбинации и представляют типы симметрии, по которым классифицируются нормальные колебания.
Нормальное колебание называется симметричным (s) по отношению к данной операции симметрии, если при ее выполнении все амплитуды естественных координат или векторы смещений атомов не меняют знака и абсолютного значения (умножаются на +1). Колебание антисимметрично (as) относительно операции симметрии, если при ее выполнении знак смещений меняется на обратный (умножение на - 1). Нормальное колебание, симметричное относительно всех операций симметрии, образующих точечную группу, к которой принадлежит молекула. Называется полносимметричным. Все остальные типы нормальных колебаний неполносимметричные или дважды (Е), или трижды (F) вырожденные.
Полная характеристика типа симметрии нормального колебания описывается его отношением ко всем операциям симметрии данной точечной группы. Невырожденные типы симметрии обозначаются А или В. При этом А используется для обозначения колебаний, симметричных относительно выделенной главной оси, ориентируемой вертикально, и колебаний при отсутствии осей симметрии – группы Cs (Iи σ), Сi(Iи i), а В – антисимметричных относительно такой оси. Подстрочные индексы g и u при А и В обозначают соответственно симметричное и антисимметричное колебания по отношению к операции инверсии в центре i. Подстрочные цифровые индексы 1 и 2 обозначают симметричный и антисимметричный типы по отношению к операции отражения в вертикальной плоскости σv, в которой лежит ось, или по отношению к повороту вокруг оси второго порядка С2, перпендикулярной к главной оси. Надстрочные индексы – один штрих (΄) или два штриха (˝) при прописных буквах – обозначают симметричный и антисимметричный типы колебаний относительно отражений в горизонтальной плоскости σh, перпендикулярной оси симметрии и в точечной группе СS. Цифровые индексы 1,2,3 используются также при символах вырожденных колебаний E и F, но не имеют того же смысла, что для невырожденных колебаний.
В терминах теории групп принадлежность нормального колебания к какому-то типу симметрии соответствует принадлежности к определенному неприводимому представлению данной группы. Вообще представлением группы называется совокупность линейных преобразований координат, соответствующих операциям симметрии точечной группы. Оно является приводимым, если для него можно выбрать координаты так, чтобы они преобразовывались раздельно. Представление называется неприводимым, если его нельзя дальше упростить, то есть нельзя выбрать новые координаты, которые преобразовывались бы раздельно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.