Определение симметрии молекул из анализа их колебательных спектров, страница 2

Вводимые для описания колебаний молекулы естественные координаты разбиваются на совокупности симметрично эквивалентных координат, переводимых операциями симметрии при равновесной конфигурации друг в друга.

Общее число координат симметрии равно общему числу естественных координат, а для определения числа координат симметрии данного неприводимого представления, то есть для подсчета числа нормальных колебаний каждого типа симметрии, необходимо знать свойства приводимых и неприводимых представлений. Это так называемые характеры представлений, то есть суммы диагональных элементов матриц преобразований координат. В теории групп выводится следующая формула:

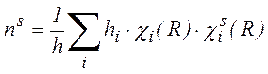,                                                     (1)

где - число колебаний типа симметрии s, в которое могут входить вместе с настоящими и ненастоящие колебания (трансляции и вращения);

h – число операций симметрии в группе (порядок группы);

 - число операций в i – том классе;

 - характер приводимого представления для операции R (в i – том классе):

 - характер неприводимого представления для операции R (в i – том классе).

Суммирование ведется по всем классам, при всех h_i = 1 – по всем операциям симметрии группы.

Характеры приводимых представлений молекулы для различных операций симметрии находятся по формулам:

χ(1) = 3N,

χ(σ) = N_σ,

χ(i) = -3N_i,

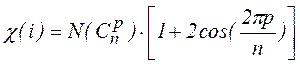,                                                             (2)

,

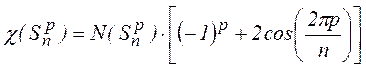где N – число атомов в молекуле;

N_σ , N_i , , - числа атомов молекулы, не меняющих своего положения при выполнении соответствующих операций симметрии.

Характеры неприводимых представлений по операциям симметрии или типы симметрии колебаний даны для всех точечных групп в таблицах. В таких таблицах кроме операций симметрии, образующих данную точечную группу, и характеров приводятся и правила отбора для ИК и КР спектров, а также указывается, к какому типу симметрии относятся трансляции и вращения относительно системы главных осей.

Как известно, для проявления колебательного квантового перехода в ИК спектре правила отбора требуют, чтобы была отлична от нуля хотя бы одна из проекций матричного элемента электрического дипольного момента данного перехода. Для этого достаточно, чтобы тип симметрии нормального колебания совпадал с типом симметрии трансляций в направлении одной из декартовых координат Т_x ,Т_y ,Т_z. Для определения правил отбора в спектре КР надо знать, к каким типам симметрии относятся компоненты тензора поляризуемости  (где i,j=x,y,z), которые преобразуются так же как и произведения координат xx, yy, zz, xy, xz, yz.

Порядок выполнения работы

1  Рассмотреть возможные структурные модификации молекулы XY₃, соответствующие точечным группам симметрии:

А)  - тригональная пирамида;

B)  - равносторонний треугольник;

C)  - равнобедренный треугольник.

2  Воспользовавшись формулами (1) и (2), а также таблицами типов симметрии и характеров неприводимых представлений группы , определить суммарное число колебаний, трансляций и вращений , относящихся к каждому  s – тому  типу симметрии.

3  Пользуясь таблицами типов симметрии, определить истинное число нормальных колебаний ()^* = , соответствующих s –тому типу симметрии. Здесь  - число трансляций T^s и вращений R^s, обладающих s –тым типом симметрии.

4  Определить число колебаний, активных в ИК и КР спекрах, пользуясь данными таблицы типов симметрии.

5  Проделать пункты 2-4 для групп симметрии  и .

6  По ИК и КР спектральным данным, указанным преподавателем, определить, к какой из перечисленных групп симметрии относится молекула XY₃.

ТАБЛИЦЫ ТИПОВ СИММЕТРИИ И ХАРАКТЕРОВ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ

	I				Активно в ИК	Активно в КР
А1	1	1	1	1	Tz	xx,yy, zz
А2	1	1	-1	-1		xy	Rz
В1	1	-1	1	-1	Tx	xz	Ry
В2	1	-1	-1	1	Ty	yz	Rx

	I			Активно в ИК	Активно в КР
A1	1	1	1	Tz	(xx+yy), zz
A2	1	1	-1		(xx-yy), zz	Rz
E	2	-1	0	Tx,, Ty	yy, xz	Rx, Ry

	I						Активно в ИК	Активно в КР
	1	1	1	1	1	1		(xx+yy), zz
	1	1	-1	1	-1	-1
	1	1	1	-1	1	-1			Rz
	1	1	-1	-1	-1	1	Tx
	2	-1	-1	0	2	0	Tx, Ty	(xx-yy), zz
	2	-1	1	0	-2	0		xz, yz	Ry,Rx

Литература

1.  Л.В. Вилков, Ю.А. Пентин. Физические методы исследования в химии. - М., 1987.

2.  2.К. Бенуэлл. Основы молекулярной спектроскопии. - М., Мир, 1985.

3.  А.А. Мальцев. Молекулярная спектроскопия. - М., 1980.

4.  Г.Н. Жижин, Б.Н. Маврин, В.Ф. Шабанов. Оптические колебательные спектры кристаллов. - М., 1984.