Определение параметров импульсов. Исследование модулированных колебаний

РАЗДЕЛ  І.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ИМПУЛЬСОВ

      Существует ряд представлений сигнала. Наиболее известное представление-зависимость амплитуды сигнала от времени в виде S=S(t), где S - сила токаi, напряжение U, напряжённость электрического E либо магнитного H поля, потенциал поля φ и другие величины. При измерении параметров сигналов все эти величины, в конечном счёте преобразуются в ток измерительного преобразователя, прохождение которого через элементы измерительных систем характеризуются его частотными характеристиками. В связи с этим широко используется частотно-спектральное представление сигналаG=G(w), выражающее зависимость амплитуды спектральной составляющей Gот частоты этой составляющей w. Частотное и временное представления сигнала связаны преобразованием Фурье:

 Если                             S(t) ÛG(w) то

                                     S(t )= = 

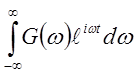
 а                                  G(w )=  =

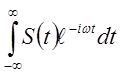
Здесь и   - операторы прямого и обратного преобразования Фурье.

   У периодических функций спектр дискретен

                                          G(w) = G(nn_o) =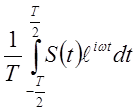

       n_o = T^-1 - минимальное расстояние между точками спектра на оси частот, n=0,1,2…  целые числа.

      Для преобразования Фурье справедлив закон сохранения энергии сигнала, который выражает

Теорема Парсеваля

                                          =

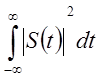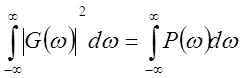
            - P(w) -спектр мощности сигнала.

  Важное при исследовании сигналов, в особенности статистических (шумовых), имеет применение функции взаимной корреляции, характеризующей степень подобия двух сигналов S(t) и  S^/(t-t)

                                                R_ss(t) =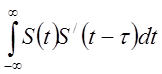  

и автокорреляционной функции

                                               R_ss(t)  =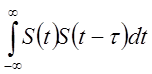 

  характеризующей  отдельный сигнал.

   Для периодической функции автокорреляционная функцияявляется чётной и R(0) представляет собой квадрат эффективного значения сигнала. Связь между спектром мощности импульса и его автокорреляционной  функцией устанавливает

Теорема Винера -Хинчина

                                                         R_ss(t)  ÛP(w)

   В ряде случаев обработка сигналов осуществляется средствами вычислительной техники. При этом производится дискретизация сигнала, т.е. измерение его через определённые промежутки времени и представление в виде дискретного набора значений. При этом интегральное преобразование Фурье трансформируется к дискретному

                                     

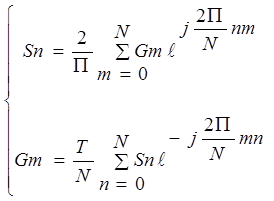
Дискретизация приводит к периодическому повторению вычисляемого спектра с частотой 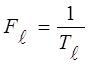 . Для того, чтобы это повторение не приводило к наложению спектра, должны выполнятся условия, которые определяет

 Теорема Шеннона:

для того, чтобы периодическое повторение спектра, вызванное дискретизацией сигнала, не измеряло повторяемый спектр, необходимо и достаточно выполнение неравенства

F_l ³ 2F_m

         -Fм - максимальная частота спектра сигнала.

      Выделяют ряд типов сигналов.

Гармоническое колебание описывается математическим выражением вида

                                            S(t) = A₀sin(2pF₀t + j₀),    F₀ =

где  - амплитуда, - частота, - начальная фаза, - период колебания.

        Импульсом называется электрическое колебание, значения которого существенно от нуля в течение ограниченного интервала времени

 Периодическая последовательность импульсов - это последовательность повторяющихся с периодом T одиночных импульсов S(t).

Для периодической последовательности прямоугольных импульсов длительностью параметрами являются скважность Q= T/tи коэффициент заполнения  G=Q^-1

     Модуляцией называется изменение во времени по заданному закону каких-либо параметров периодических колебаний, если это изменение мало за период колебаний. Число возможных видов модуляции равно числу параметров модулируемого колебания (амплитудная, частотная, фазовая модуляции). При амплитудной модуляции высокочастотного сигнала U(t) = A₀sin2pf₀t низкочастотным сигналомU(t) = A₀sin2pF₀t модулированное колебание имеет вид (рис.4)

                                      U_ам(t) = A₀(1+m sin2pF₀t)sin2pf₀t  

где A₀- амплитуда несущей, имеет смысл среднего значения огибающей за период модуляции  T₀=1/F₀

        - несущая частота ;

        - частота модуляции ;

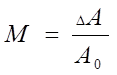 - коэффициент  глубины модуляции при АМ.

     В соответствии с рис.

                                                  

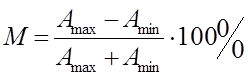
  При частотной модуляции сигнала U(t) = A₀sin2pf₀t низкочастотным сигналомU(t) = A₀sin2pF₀t  результирующее колебание(ЧМ) имеет вид (рис.):

                                  U_чм(t) = A₀sin(2pf₀t +sin2pF₀t

   - амплитуда колебания ;

   - частота модуляции ;

   - средняя частота за период модуляции 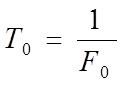 или частота при отсутствии модуляции ;

    - девиация, имеющая смысл максимального отклонения мгновенной частоты  от её среднего значения ;

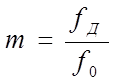  - индекс модуляции

   Произвольный периодический сигнал с периодом   T  описывается функцией вида