















Лабораторная работа № 2
Определение оптических характеристик тонких
пленок
Цель работы: освоить методику измерения спектров просекания тонких диэлектрических пленок в видимой области. Определить оптические постоянные тонких пленок, используя спектральную интерференционную кривую пропускания.
Приборы и принадлежности: спектрофотометр СФ-46, тонкие пленки
SiO![]() ,In
,In![]() O
O![]() ,MgF
,MgF![]() ,IrO
,IrO![]() , нанесенные на подложки из NaCl, стекла К8,
кварца С5-1.
, нанесенные на подложки из NaCl, стекла К8,
кварца С5-1.
Теоретическоевведение
При получении
тонкопленочных покрытий, используемых в качестве функциональных элементов оптики,
микроэлектроники и др. областей науки и техники, важной задачей является
определение их оптических свойств. К настоящему времени разработано множество
методов определения оптических констант - показателя преломления n и коэффициента
поглощения ![]() , использующих
в своей основе различные экспериментальные параметры, различающихся областью
применения, точностью и т.д. Рассмотрим некоторые из них.
, использующих
в своей основе различные экспериментальные параметры, различающихся областью
применения, точностью и т.д. Рассмотрим некоторые из них.
1. Эллипсометрия.
Для того, чтобы охарактеризовать с оптической точки зрения тонкую изотропную пленку, необходимо указать значения оптических
постоянных
n и ![]() , материала а также ее толщину d. Метод эллипсометрии основан на измерении параметров, описывающих состояние
поляризации
отраженного от исследуемой пленки света. Поскольку
плоскополяризованный
свет после отражения оказывается эллиптически-поляризованным, понятно происхождение названия этого метода. С помощью эллипсометра определяются сдвиги фаз при отражении световых волн, поляризованных параллельно плоскости падения
, материала а также ее толщину d. Метод эллипсометрии основан на измерении параметров, описывающих состояние
поляризации
отраженного от исследуемой пленки света. Поскольку
плоскополяризованный
свет после отражения оказывается эллиптически-поляризованным, понятно происхождение названия этого метода. С помощью эллипсометра определяются сдвиги фаз при отражении световых волн, поляризованных параллельно плоскости падения ![]() и перпендикулярно плоскости падения
и перпендикулярно плоскости падения ![]() , а также относительный
азимут
эллипса поляризации отраженного света
, а также относительный
азимут
эллипса поляризации отраженного света ![]() . Эти экспериментальные параметры связаны оптическими параметрами пленки:
. Эти экспериментальные параметры связаны оптическими параметрами пленки:
![]() tg
tg ![]() e
e![]() =
=![]() ,
(1)
,
(1)
![]()
![]() ;
;
где
![]() =f(n,
=f(n,![]() ,d),
,d), ![]() =f’(n,
=f’(n,![]() ,d)
,d)
- комплексные коэффициенты отражения для параллельно и перпендикулярно поляризованного света.
Выражение
(1) является уравнением для комплексных величин, которое разбивается на два
уравнения - для действительной и мнимой составляющих. Т.е., решив уравнение
(1), можно найти значения двух величин, например n и ![]() , если d определено из
независимых измерений. Все три величины n, и
, если d определено из
независимых измерений. Все три величины n, и ![]() и d могут быть
определены по
и d могут быть
определены по ![]() и
и ![]() , измеренных при двух
различных углах падения.
, измеренных при двух
различных углах падения.
2. Метод Крамерса-Кронига
Этот
метод применим для поглощающих пленок, для которых комплексный показатель
преломления ![]() полностью
описывает оптические
полностью
описывает оптические
свойства среды при заданной толщине пленки d :
![]() = п - i
= п - i![]()
Метод позволяет
определить n и ![]() в широкой спектральной области
на основе измерения одного из спектров - спектра отражения R(
в широкой спектральной области
на основе измерения одного из спектров - спектра отражения R(![]() ) или спектра пропускания T(
) или спектра пропускания T(![]() ) , что выгодно отличает его от других
методов, требующих большего числа измеряемых величин.
) , что выгодно отличает его от других
методов, требующих большего числа измеряемых величин.
Комплексный
коэффициент отражения на частоте ![]() может быть представлен в виде:
может быть представлен в виде:
![]() (
(![]() )=[R(
)=[R(![]() )]
)]![]() e
e ![]() ,
(2)
,
(2)
где R(![]() )- измеряемое значение коэффициента отражения (по мощности)
)- измеряемое значение коэффициента отражения (по мощности)
на частоте ![]() ;
; ![]() - фаза комплексного коэффициента отражения. Фаза
Ф и амплитуда R комплексного
коэффициента отражения связаны между собой соотношением Крамерса-Кронига:
- фаза комплексного коэффициента отражения. Фаза
Ф и амплитуда R комплексного
коэффициента отражения связаны между собой соотношением Крамерса-Кронига:
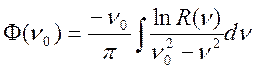 (3)
(3)
Оптические
постоянные n и ![]() рассчитываются из формулы Френеля,
которая, например для S -поляризации света имеет вид:
рассчитываются из формулы Френеля,
которая, например для S -поляризации света имеет вид:
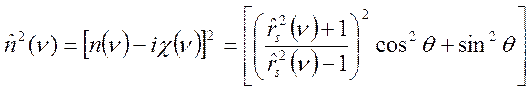 (4)
(4)
где ![]() - угол падения света.
- угол падения света.
Таким
образом, измерив спектр отражения R(![]() ) в диапазоне частот от
) в диапазоне частот от ![]() до
до ![]() и экстраполируя функцию R(
и экстраполируя функцию R(![]() ) за пределы диапазона измерений от
) за пределы диапазона измерений от ![]() до 0 и от
до 0 и от ![]() до
до ![]() , в соответствии с формулой (3) рассчитывают
значения фазы Ф(
, в соответствии с формулой (3) рассчитывают
значения фазы Ф(![]() ) во всем
спектральном диапазоне. Найденный таким образом комплексный коэффициент отражения
на частях исследуемого диапазона ( см (2)) используется для расчета
) во всем
спектральном диапазоне. Найденный таким образом комплексный коэффициент отражения
на частях исследуемого диапазона ( см (2)) используется для расчета ![]() и
и ![]() из выражения (4).
из выражения (4).
Погрешность
в расчете n и ![]() обусловлены экспериментальными
погрешностями
обусловлены экспериментальными
погрешностями ![]() и
и ![]() при измерении коэффициента
отражения и угла
при измерении коэффициента
отражения и угла
падения,
а также погрешностью расчёта фазы ![]() , источником которой являются:
, источником которой являются:
а)
ограниченность интервала измерений ![]() и связанная с этим экстраполяция R(
и связанная с этим экстраполяция R(![]() ) за пределы области измерений;
) за пределы области измерений;
б)
наличие особой точки (![]() ) подынтегральной функции в выражении (3).
) подынтегральной функции в выражении (3).
В
настоящее время имеется ряд различных способов экстраполяции R(![]() ) , а также способы устранения
необходимости экстраполяции за счет коррекции полученного при интегрировании в
пределах от
) , а также способы устранения
необходимости экстраполяции за счет коррекции полученного при интегрировании в
пределах от ![]() до
до ![]() решения. Например, функция n
решения. Например, функция n![]() представляется в виде
представляется в виде
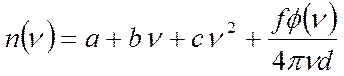 ,
,![]()
где
a, b, c, f - константы,
которые определяются из условия миминизации величины ![]() , d - толщина пленки.
, d - толщина пленки.
Погрешности
значений n и ![]() при этом снижается до 5% при
погрешности
при этом снижается до 5% при
погрешности
Измерений
R![]() .
.
3. Для поглощающей
плёнки на прозрачной подложке разработан метод расчета оптических постоянных ![]() и
и ![]() на основе экспериментальных спектров отражения R(
на основе экспериментальных спектров отражения R(![]() ) и пропускания
) и пропускания ![]() . При учете многократного отражения
света в плоскопараллельном слое пленки интерференции коэффициенты R и T на заданной
частоте
. При учете многократного отражения
света в плоскопараллельном слое пленки интерференции коэффициенты R и T на заданной
частоте ![]() выражаются:
выражаются:
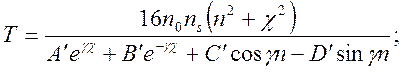
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.