Определение удельного заряда электрона методом магнетрона (Лабораторная работа № 3)

Лабораторная работа №3

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА.

Цель работы: Изучить движение заряженных частиц в магнитном поле и измерить удельный заряд методом магнетрона.

Теоретические сведения.

В настоящей работе удельный заряд электрона или отношение  для электрона определяется с помощью «метода магнетрона». Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей подобно конфигурации полей в магнетронах-генераторах электромагнитных колебаний СВЧ.

          Установка содержит электронную лампу с коаксиальными цилиндрическими электродами, помещённую внутри соленоида. При пропускании через соленоид электрического тока внутри лампы возникает магнитное поле, вектор индукции которого параллелен оси электрода. Термоэлектроны, испускаемые катодом, движутся под действием двух взаимно перпендикулярных полей: электрического поля анода, силовые линии которого направлены радиально, и магнитного поля, создаваемого соленоидом. Проанализируем движение электронов в лампе, когда радиус катода пренебрежимо мал по сравнению  с катодом по сравнению с радиусом анода. При этом электрическое поле в лампе является сильно неоднородным, плотность силовых линий и следовательно, напряжённость поля быстро убывает по мере удаления от катода. Движение электронов в лампе можно разбить на два этапа: сначала быстрое ускорение электрическим полем в области, прилегающей к катоду, где в основном происходит падение анодного напряжения, затем движение в магнитном поле с практически постоянной по модулю скоростью по траектории, близкой к окружности. Пренебрегая начальной скоростью испускаемых термоэлектронов, ск5орость их движения по окружности можно найти из закона сохранения энергии

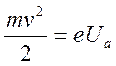                                                                                     (3.1)

где U_a – анодное напряжение. Центростремительное ускорение при движении по окружности сообщается электрону силой Лоренца . Используя уравнение движения электрона mV²/r = qB и (3.1) находим радиус траектории электрона

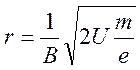                                                                                  (3.2)

Из выражения (3.2) следует, что по мере возрастания индукции магнитного поля происходит всё более сильное искривление электронов. При некотором, так называемом критическом значении индукции B_кр, траектории электронов будут касаться поверхности анода, то есть будет

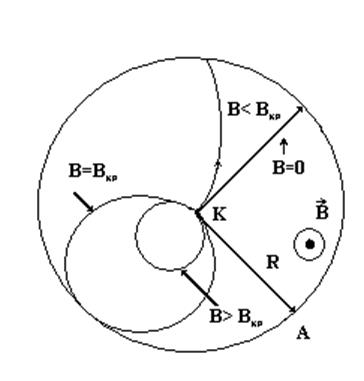выполнятся соотношение r = R_a/2, где R_a - радиус анода ( см. рисунок 3.1).

                                                              Рисунок 3.1 

Если при значениях индукции магнитного поля B< B_кр все испускаемые катодом термоэлектроны достигают анода, то при значениях индукции   B> B_кр все электроны в следствие сильного искривления их траектории возвращаются к катоду. Поэтому ток должен резко исчезать при критическом значении индукции магнитного поля(штриховая линия на рисунке 3.2).

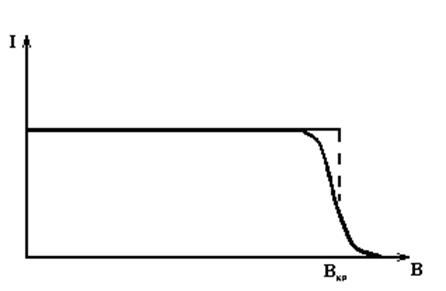                                                        Рисунок 3.2   

Однако в следствие того, что испускаемые катодом термоэлектроны имеют различные начальные скорости, уменьшение анодного тока при росте индукции магнитного поля происходит более плавно(сплошная линия на рисунке 3.2). При этом наиболее быстрое уменьшение анодного тока по-прежнему соответствует критическому значению индукции магнитного поля.

          Из формулы (3.2) следует соотношение

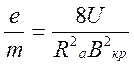                                    ,                                             (3.3)

позволяющее определить удельный заряд электрона методом магнетрона. Связь между индукцией магнитного поля внутри лампы и силой тока соленоида можно найти с помощью закона Био-Савара-Лапласа

                                   

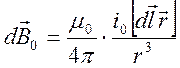
Здесь  - вектор индукции магнитного поля, создаваемого элементом  кругового тока,  - сила тока,  - физически бесконечно малый вектор, касательный к окружности, направление которого совпадает с направлением тока,  - радиус-вектор, проведённый от данного элемента тока в точку наблюдения (рисунок 3.3), квадратные скобки обозначают векторное произведение.

                                                   Рисунок 3.3

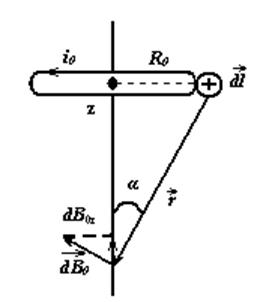Векторы , соответствующие различным элементам кругового тока, образуют коническую поверхность с вершины точки наблюдения, и суммарный вектор индукции магнитного поля кругового тока направлен вдоль оси z. Вычисляя проекцию вектора  на ось z , учитывая, что векторы и взаимно ортогональны и интегрируя по окружности, получаем

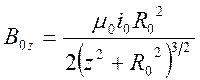                                                                         (3.4)

где z – координата центра витка тока,  – радиус витка. Наибольший отрезок соленоида длиной dz (рисунок 3.4) эквивалентен круговому току , где I – сила тока в соленоиде, - количество витков на выбранном участке соленоида, n– линейная плотность витков. Производя замену переменной  и интегрируя соотношение (3.4) по всему соленоиду, находим индукцию магнитного поля в произвольной точке О на оси соленоида: