Основы автоматизированных расчётов мостовых переходов, страница 3

,                (5)

                                   0 < x < l_i.

Целью расчёта является определение неизвестных коэффициентов α_i  и β_i на каждом элементе i. Для этого каждому элементу ставится в соответствие некоторый функционал. В частности в задачах на прочность и устойчивость в качестве такого функционала используется выражение для полной потенциальной энергии П. Решение задачи находится в том случае, когда потенциальная энергия достигает минимума, т.е.

 .                                                         (6)

Определив коэффициенты α_i  и β_i на всех конечных элементах модели объекта, мы тем самым находим интересующую нас характеристику (напряжения или перемещения)  во всём сооружении.

4 Температурные расчёты мостов

Результаты обследований эксплуатируемых железобетонных мостов со сроками службы, близкими к нормируемым, показывают, что 80 % из них имеют дефекты. Серьёзные дефекты возникают в зонах, где действуют наибольшие температурные напряжения. Это приводит к нарушению сплошности и герметичности бетона защитного слоя.

Температурное поле описывается уравнением теплопроводности

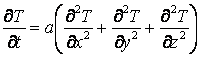 .                                       (7)

где

а – коэффициент температуропроводности;

Т – температура;

t – время;

x, y, z – пространственные координаты.

Коэффициент температуропроводности определяется теплофизическими константами материала сооружения и вычисляется по формуле

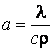,                                                                    (8)

где

λ – коэффициент теплопроводности,

с – удельная теплоёмкость,

ρ – плотность.

Для замыкания задачи на границах, т.е. поверхности моста, должны быть заданы краевые условия.

Начальное условие:

 ,                                                (9)

т.е. при t=0 известно температурное поле в сооружении.

На границе соприкосновения двух твёрдых тел задаётся известная температура (граничное условие первого рода):

                                                          (10)

или поток тепла (граничное условие второго рода)

.                                                             (11)

На границе твёрдого тела и окружающей среды (граничное условие третьего  рода)

,                                                         (12)

где

α – коэффициент теплопередачи (принимается из экспериментов),

Т_в – температура воздуха,

Т_с – температура на границе тела.

Для решения такой задачи используется метод конечных элементов. Структура конечных элементов при определении температурного поля и поля напряжений может быть принята одинаковой. В качестве функционала – температурный баланс.