Основы автоматизированных расчётов мостовых переходов, страница 2

Данная система дифференциальных уравнений решается методом конечных разностей (МКР), в котором производные заменяются конечными разностями, непрерывные координаты и функции – дискретными. Заменим какую-либо производную конечной разностью, например, .  Согласно определению производной

,

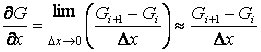где .

Тогда система дифференциальных уравнений (1)-(3) превращается в систему алгебраических уравнений.

3 Расчёты мостов по методу предельных состояний

В нашей стране расчёты конструкций на прочность и устойчивость осуществляются по методу предельных состояний. Его суть заключается в том, что из всего множества возможных состояний объекта выбираются и проверяются лишь предельные, которые могут возникнуть при самом неблагоприятном сочетании нагрузок и воздействий. В общем виде условие непревышения предельного состояния может быть записано как

Ф(F_н, R_н,γ_f, γ_m, γ_n, γ_c) ≥ 0 ,                                             (4)

где

F_н – нормативное значение обобщённого силового воздействия,

R_н – нормативное значение несущей способности,

γ_f  – коэффициент надёжности по нагрузкам,

γ_m – коэффициент надёжности по материалам,

γ_n – коэффициент ответственности сооружения,

γ_c – коэффициент условий работы.

Существуют два подхода к расчётам по предельным состояниям моста. Первый подход более простой и заключается в расчленении моста на самостоятельные элементы (плиты, главные балки, диафрагмы, опоры). Достоинства метода – простота и наглядность. Расчёты могут быть выполнены вручную с эпизодическим применением компьютеров. Недостатком данного подхода является то, что результаты расчётов могут оказаться неточными. Обычно эта неточность идёт в запас прочности, т.е. ведёт к утяжелению конструкции, перерасходу материалов.

Второй подход к расчётам конструкций базируется на широко известном численном методе – методе конечных элементов (МКЭ). Он в настоящее время широко распространён и применяется от анализа напряжений в бетонных конструкциях до атомных станций и космических кораблей.

Суть метода конечных элементов заключается в том, что любой объект (конструкция) самой сложной формы представляется совокупностью некоторых элементов, имеющих конечные размеры (конечные элементы). В их качестве берутся простые геометрические фигуры – прямоугольники, треугольники (в случае постановки плоской задачи), параллелепипеды, тетраэдры (в случае постановки пространственной задачи). Для мостов может быть применима и самая простая постановка задачи – замена моста стержневой системой, т.е. в качестве конечных элементов рассматривается отрезок. Эти элементы взаимодействуют между собой в вершинах  элементов. Чем мельче элемент, тем точнее аппроксимация объекта конечными элементами.

Рассмотрим вантовый мост (см. рис. 3). В самой простейшей модели конечным элементом является стержень, т.е. одномерный конечный элемент.

Рисунок 3 – Вантовый пешеходный мост в г. Красноярске

Стержневая система приведена на рисунке 4.

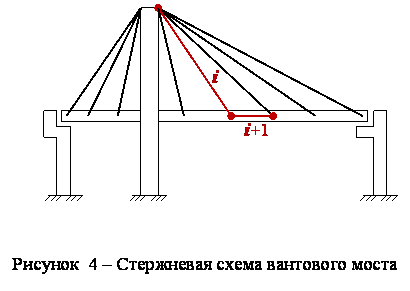
Любая характеристика мостового сооружения φ (напряжения, перемещения, температура) представляет собой непрерывную функцию, областью определения которой является поверхность (объём в трёхмерной постановке задачи) всего объекта. Вводя конечные элементы, мы тем самым от непрерывной функции φ переходим к дискретной функции φ_i, у которой значения задаются только в узлах элементов.   В промежутке между узлами (на i-м элементе длиной l_i) значение