Математика \ Математический анализ

Монотонные последовательности. Лемма о вложенных отрезках. Сходимость монотонной ограниченной последовательности в R, страница 2

D1

.

 

.

.

D2

.

 

.

.

D3

.

 

.

.

D4

.

 

.

Разделим [ – M ; M] пополам. Если в правой половине имеются точки последовательности (xn), то обозначим ее через D1, если нет, то через D1 обозначим правую половину, если в ней имеются точки (xn), и левую половину, если в правой нет точек (xn).

Продолжая этот процесс, получим последовательность отрезков Dn такую, что " n Î NDn É Dn+1. Очевидно, |Dn| = M / 2n-1; lim |Dn| = lim (M / 2n-1) = 0.

Таким образом, последовательность отрезков Dn удовлетворяют двум условиям леммы о вложенных отрезках, следовательно, существует C, принадлежащая всем отрезкам Dn.

Шаг 3.Теперь докажем, что lim xn = C.

Докажем противное, то есть пусть lim xn ¹ C. Это означает, что $ e > 0 такое, что |xn – C| ³ e выполняется для бесконечного числа номеров n. Но тогда найдется такой отрезок Dk ' C, вне которого находится бесконечное число членов последовательности (xn). Таким является отрезок Dk у которого |Dk| < e.

C – e                 C                  C – e  

                          Dk

            Однако, это ведет к противоречию, поскольку  справа от Dk точек последовательности (xn) нет по построению, а слева от Dk может быть только конечное число точек xn в силу того, что последовательность (xn) возрастает.  

11.4 Сходимость монотонной последовательности в R.

Теорема. Любая монотонная последовательность сходится в R.

*  Случай, когда xn = 0 (1), рассмотрен ранее.

Если xn ¹ 0 (1), то lim xn = +¥ в случае возрастающей последовательности (xn) и lim xn = –¥ в случае убывающей последовательности (xn). 

11. 5 Число e. Будем считать известным:

1) b1 + b1q + … + b1qn-1 = ;

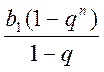2) (a + b)n =

Рассмотрим последовательность

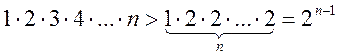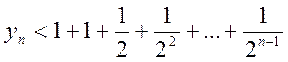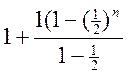Очевидно, что она строго возрастает, то есть " n Î N yn < yn-1. Так как n! = , то  = < 3.

Таким образом, последовательность (yn) строго возрастает и ограничена и, в силу m. Вейерштрасса, имеет предел

lim yn = e, 2 < e £ 3.

Покажем, что этот же предел имеет последовательность xn = (1+)n.

По формуле Ньютона

xn = (1+)n = .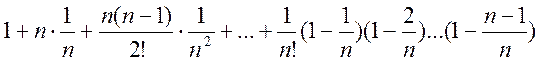

Отсюда следует:

1) xn < yn;

2) (xn) – строго возрастающая последовательность.

Свойство 2) вытекает из того, что xn+1 отличается от xn (n+2)-м положительным членом и заменой множителей вида 1 –  большим множителем 1 – 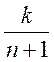. Следовательно, к последовательности (xn) можно применить теорему Вейерштрасса в силу которой $ x0 Î R такое, что lim xn = x0.

Докажем, что x0 = e.

С этой целью заметим, что " m > n

xm > 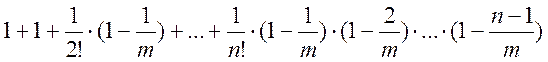, так как по сравнению с выражением, стоящим справа, у xm есть еще положительные слагаемые.

При фиксированном n устремим m к бесконечности, тогда из предыдущего неравенства получим x0 ³ yn.

В результате, приходим к двойному неравенству xn £ yn £ x0.

На основании принципа двустороннего ограничения при n ® ¥ получаем lim xn £ lim yn £ lim x0 или x0 £ e£ x0, что равносильно равенству x0 = e.

Итак, .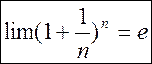

11.6 Доказательство иррациональности числа e.

Предположим, что e Î Q, то есть e =. Тогда q!eÎ N. Так как lim yn = e, то
q!e = q! (1+1+…+) + lim .

Так как 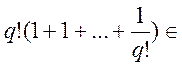N, то lim (        ) тоже целое число!

В то же время,

= £

== ®

.

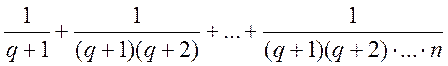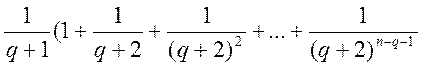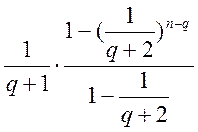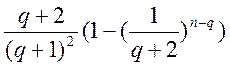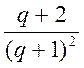Но для " q Î N 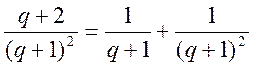 £  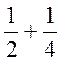< 1, то есть lim (        ) Ï N. Данное противоречие доказывает иррациональность числа e.

Скачать файл