Метод Эйлера и его модификации

МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ ОДУ 1-ГО ПОРЯДКА.

1. МЕТОД ЭЙЛЕРА И ЕГО МОДИФИКАЦИИ.

             Большинство задач физики, в которых рассматривается поведение одной величины в зависимости от изменения другой, сводится к математической задаче решения обыкновенного дифференциального уравнения (ОДУ). Многие дифференциальные уравнения, возникающие в прикладных задачах, не решаются аналитически. Поэтому универсальными, а в большинстве случаев и единственными методами решения ОДУ являются численные методы. Настоящая лабораторная работа посвящена изучению и применению простейших одношаговых численных методов решения задачи Коши для ОДУ 1-го порядка.

             Задача Коши заключается в нахождении функции y(f) по заданному ДУ и начальному условию:

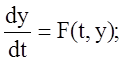
                                                                             ;                                                (1)       

                                                           ;                                                 

для решения которой на интервале [a,b] c достаточно малым шагом h строится система равноотстоящих точек

                                                                                                           (2)

                                                                      

В одношаговых численных методах значения приближённого решения вычисляются последовательно от точки к точке, начиная с , причём для вычисления решения на i-ом шаге используется значение решения, найденного на предыдущем (i-1)-м шаге.

              Наиболее простым и наглядным методом решения задачи (1) является метод Эйлера. Для получения приближённого решения дифференциального уравнения 1-го порядка в методе Эйлера используется приближённая конечно-разностная аппроксимация производной в точке .

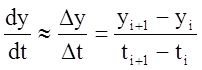                                                                                                         (3)

где  - решение уравнения в точке . Так как в простейших методах обычно выбирают постоянный шаг между точками

                                                                       

то, подставляя в (1) конечно-разностное значение производной (3), получаем в точке  

                                                    

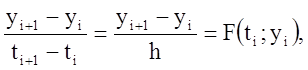
откуда следует

                                                                                                        (4)

Используя начальные значения   можно последовательно найти приближённые значения функции y(t) в узловых точках

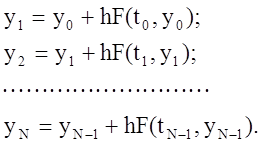                                                                                                (5)

Для программирования таких вычислений достаточно описать массивы для хранения значений  и , и организовать цикл по i.

           Метод Эйлера обладает исключительной простотой, однако имеет малую                                               точность, что резко ограничивает возможности его применения. Для получения более точных результатов обычно используют следующие модификации метода Эйлера:

           1) Метод Эйлера-Коши. На каждом шаге вначале вычисляется первое приближение

                                                                                                              (6)

а затем на этом же шаге находится более точное приближение

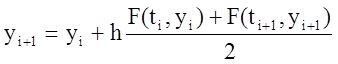                                                                                     (7)

            2) Улучшенный метод Эйлера. На каждом шаге сначала вычисляются промежуточные значения:

                                                               

                                                                                                  (8)

а затем полагают

                                                                                                    (9)

По сравнению с обычным методом Эйлера его модификации обладают значительно более высокой точностью.