Конечноразностная аппроксимация граничной задачи

   СУРС №11    Выполнил студент гр.Ф-31 Черныш В.В.                 

   Лекция 14.  Решение граничной задачи для ОДУ - 2 методом прогонки.

§1.  Конечноразностная апроксимация граничной задачи.

Мы продолжаем применение метода конеч. разностей к реш-ю грани задачи, кот. начата на предыдущей лк. (13.17)-(13.19) – постановка задачи (ОДУ – 2+ГУ)

Мы ввели 3 этапа МКР:

1)  сетка (лк. 13 §3)

2)  замена производных конечно-разностными выражениями

Во внутр. узлах :

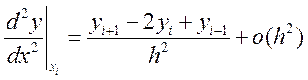                                                 ( 14.1 )        

                                                                                                       

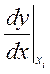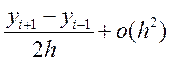                                             =      ( 14.2 )

Коэф- ты ур-я:    A()A;    B()B;     C()C;     D()D    (14.3)

Т. о. для ур-я во внутр. точках  ,  =1… 

     

Для каждого

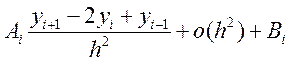
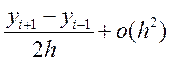   +C    (14.4)

  - это есть система () линейных ур-ний, где - изв-е числа относ-но неизв-х .

Удобно собрать коэф-ты при неизвестных

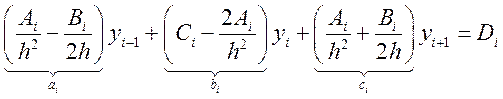   (14.5)

Введем обозначения 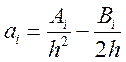   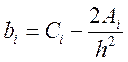;  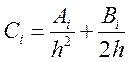  ;        (14.6) 

    (14.7)               

  Рассмотрим ГУ :              

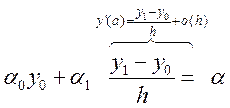
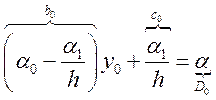         (14.8)

Т. о.       (14.9)

На второй границе

              

               

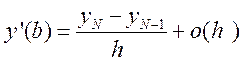
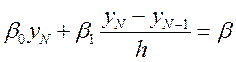
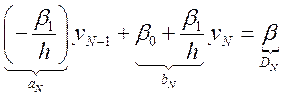        (14.10)

Т. о.          (14.11)

Учёт ур-я во внутр-х узлах сетки и граничных условий с конечно-разн-ми производными даёт нам систему () ур-ний относ-но () неизв-х

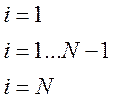
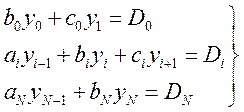                (14.12)

Эту систему можно записать в матрич. форме

                                 

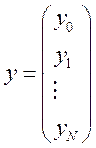
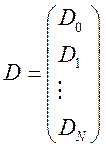
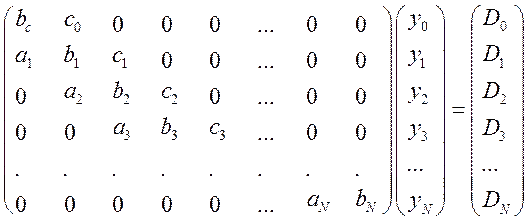                                                           (14.13)

Матрица системы ур-ний явл-ся 3-х диагональной

Такой вид матрицы опред-ся тем, что независимо от общего кол-ва неизвестных каждое ур-е связывает только 3, а нулевое и N-ное только 2 неизв-е величины. Решать систему ур-ний с 3-х диаг-ной матрицей стандартным методом Гаусса неэф-но: a) большая часть памяти будет занята нулями; б) болшая часть времени будет занята на обработку нулевых эл-тов.

   Напр:   N=1  101 неизв-х   ,    101 ур-ние

              Всех эл-тов 101101=10201 из них ненулевых 301

Поэтому для реш-я систем ур-ний с трёх диаг-й матрицей разработан спец. Метод Гаусса, обрабатывающий только ненулевые эл-ты матрицы – метод прогонки (1954г.)