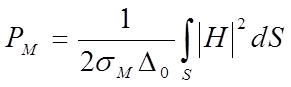Колебательные системы СВЧ-диапазона (Лабораторная работа № 4), страница 2

                                                                                  (13)

где 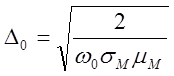  - глубина проникновения поля в стенки резонатора или глубина скин-слоя;

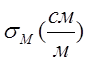   -удельная проводимость стенок резонатора;

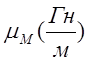       -магнитная проницаемость стенок резонатора.

Тогда частная добротность резонатора, определяемая при условии отсутствия потерь в диэлектрике и внешних цепях, найдется из выражения

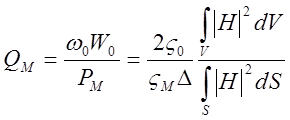                                                                               (14)

где

1.2. Потери энергии в диэлектрике

Боли резонатор заполнен диэлектриком с комплексной диэлектрической проницаемостью , где - тангенс угла диэлектрических потерь, то мощность потерь энергии в единице объема диэлектрика равна

                                                    

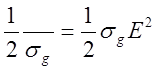
а во всем объеме за время: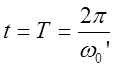

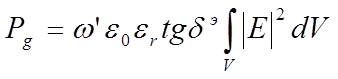                                                                          (15)

где  - резонансная частота резонатора, заполненного диэлектриком. При этом потери энергии за период колебаний составят

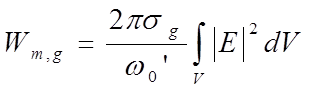                                                                             (16)

Тогда частная добротность резонатора без учета потерь в стенках и во внешних цепях определится выражением

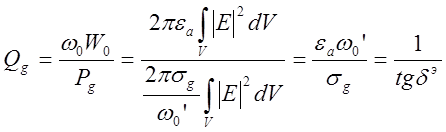                                                          (17)

1.З.Потери энергии на излучение через элементы связи с внешней цепью.

Величину 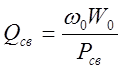 называют внешней добротностью резонатора. По смыслу она является добротностью идеализированного резонатора, потери энергии которого обусловлены одним лишь излучением во внешнее (по отношению к полости резонатора) пространство через элементы связи.

Формулу (8) часто пишут так:

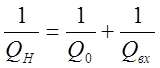                                                                                                    (18)

где -нагруженная добротность резонатора;

-внешяяя добротность резонатора;

  -собственная добротность резонатора.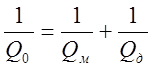  

Если ввести величину 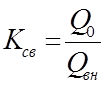,называемую коэффициентом связи резонатора с внешней цепью, то величину нагруженной и внешней добротностей можно выразить через  и собственную добротность по соотношениям

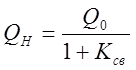
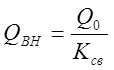                                                                                      (19)

2.Расчет собственной добротности прямоугольного резонатора

Получим формулу для собственной добротности прямоугольного резонатора с колебаниями типа Н_10Р при условии, что он заполнен воздухом

Из решения воскового уравнения для прямоугольного резонатора имеем следующие выражения, определяемые компоненты электромагнитного поля для волны Н_10Р:

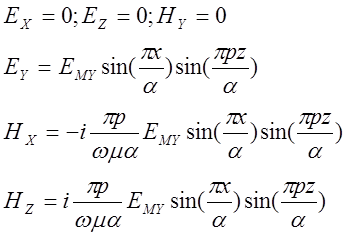                                                             (20) - (21)

где  - геометрические размеры резонатора (рис.9.)

По определению добротности, для выбранного нами случая можно записать          

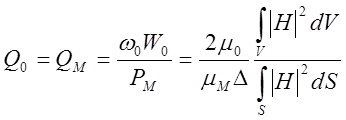                                                                        (22)

где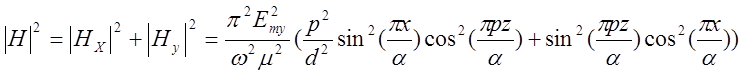     

Можно показать что 

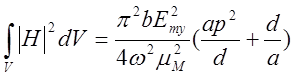                                                                                   (23)

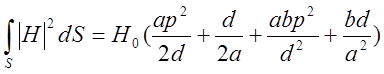                                                                      (24)

Тогда получим, что

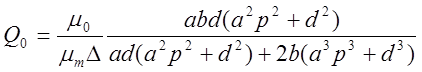                                                              (25)

где

Рассчитаем величину собственной добротности, учитывающую только потери в стенках резонатора для колебаний типа Н₁₀₁.,если известно, что а=0,12 м; в=0,057 м; f₀= 2250 МГц;  =6,1 I0⁷ См/м;

Из соотношения 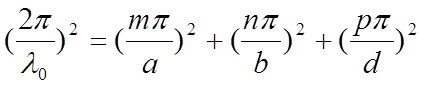 следует, что для выбранного типа колебаний Н₁₀₁, резонансная длина резонатора равна.

                                             

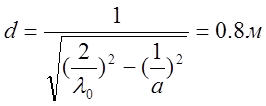
Определим значение множителя

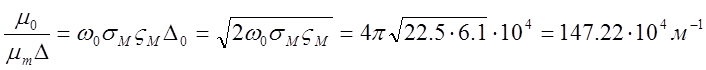
Тогда искомая величина добротности 

Из (25) следует, что с уменьшением размера "в" резонатора, не влияющего на резонансную частоту при колебаниях типа Н₁₀₁, добротность резонатора быстро падает.

Действительно, если  и, то выражение (25) принимает вид