Верхние и нижние грани числовых множеств

§ 14. Верхние и нижние грани числовых множеств.

14.1.Вступление.

R, снабженное структурой полного архимедовски упорядоченного поля, - числовая прямая.

Числовым множеством будем называть подмножества числовой прямой.

В этом параграфе будут введены понятия верхней и нижней грани числового множества, доказана лемма о верхней грани и введено понятия предела м. числового множества.

14.2. Верхние и нижние грани числового множества.

Определение 1: Числовое множество X называется ограниченным сверху, если существует такое действительное число b, что для всех xÎX выполняется неравенство: x≤b.

$bÎR   "xÎX Þ x≤b.

Примеры:

1)  {..; -2; -1; 0}; b=0.

2)  {1; ; …; ; …}; b=1.

Число b называют мажорантой множества X.

Определение 2: Числовое множество X называется ограниченной снизу, если существует такое действительное число a, что "xÎX выполняется неравенство x≥a;

A – миноранта X.

$aÎR   "xÎX Þ x≥a.

Примеры: N, Z₀, {1; ; …; ; …}

Определение 3: Числовое множество называется ограниченным, если оно ограниченно сверху и снизу.

                      

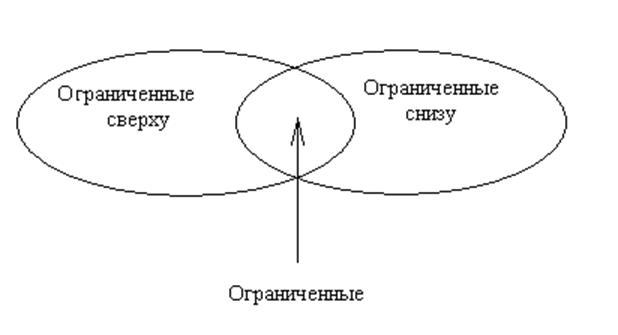
Числовая прямая не ограниченна ни сверху, ни снизу.

Определение 4: Верхней гранью ограниченного сверху числового множества X ( обознач. snp X или sup x) называется наименьшая из xÎX мажорант множества X. Если числовое множество X не ограниченно сверху, то полагают sup x=+∞.

Примеры:

sup {…,-2,-1,0}=0.

sup {1; ; …; ; …}=1.

sup N=+∞, sup .

Определение 5: Нижней гранью ограниченных снизу числового множества X (ihf X или inf x, xÎX) называется наибольшая из минорант множества X.

Если числовое множество X не ограниченно снизу, то полагают inf X=.

Примеры: inf N=1; inf Z₀=0;

inf {1; ; …; ; …}=0;

inf Z=; inf .

Верхние и нижние грани могут как принадлежать, так и не принадлежать X.

Определение 4’: Действительное число β называется верхней гранью ограниченного сверху числового множества X, если:

1)  При каждом xÎX  x≤ β;

2)  Каково бы не было ε>0 существует, по крайней мере, одно число xÎX такое, что         β- ε≤x≤β.

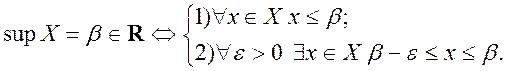
Определение 5’: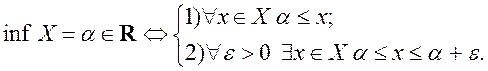

Тривиальна

Теорема:.

Другой формой выражения свойства полноты множества R служит, так называемая

14.3 Лемма о верхней грани

Лемма: Всякое непустое ограниченное сверху числовое множество X имеет конечную верхнюю грань.

◄ а) Если множество X-конечное, то верхняя грань равна наибольшему числу.

б) Пусть X-бесконечное множество.

Будем доказывать методом деления отрезков пополам. По условию, X ограниченного сверху, значит, $bÎR, такие что "xÎX  x≤b. Возьмем любой элемент x₀ÎX и рассмотрим [x₀;b].

Разделим [x₀;b] пополам. Через ∆₁ обозначим ту из его половинок, что содержит точки множества X и находится правее. Пусть ∆₁=[a₁;b₁].

Разделим ∆₁ пополам и через ∆₂ обозначим ту из его половинок, что содержит точки X и находится правее. ∆₂=[a₂;b₂]. Продолжая процесс деления получим последовательность (∆_n), удовлетворяющая двум условиям:

1)

2)

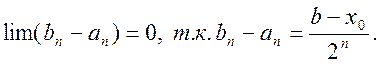
По лемме о вложенных отрезках $ единственная точка 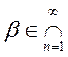 (принадлежит всем отрезкам).

1)  Пусть x – произвольная точка X. Докажем, что x≤β. Для этого предположим противное: x>β. т.к. |∆_n| = 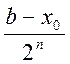, то $n такое, что x находится правее отрезка ∆_n,содержащего β, чего быть не может, т.к. по построению последовательность (∆_n) правее любого ∆_n нет точек множества X.

2)  Пусть ε>0, тогда $n такой, что точка β –ε находится левее ∆_n, а по ∆_n обязательно имеется точка множества X (по построению последовательности (∆_n)).

Итак на основании определения 4’  sup X = β.  ►

Анализ доказательства леммы показывает, что (?) доказано

Утверждение: Из всякого непустого ограниченного сверху числового множества, X можно выделить последовательность (x_n) его элементов сходящуюся к конечнойверхней грани множества X.

◄ Действительно, достаточно на любом шаге элемент x_n Î ∆_n .

Обобщением леммы о верхней грани служит

Теорема 1: Любое числовое множество имеет верхнюю грань.

◄ Для случая, когда X ограниченная теорема доказана выше. Если же множество неограниченно сверху, то согласно определению 4, sup X = +∞. ►

Аналогично доказывается лемма о нижней грани:

Лемма: Всякое непустое, ограниченное снизу числовое множество X  имеет конечную нижнюю грань.

Теорема 2: Любое числовое множество имеет конечную нижнюю грань.

14.4  Предостережение.

Не нужно смешивать верхний предел последовательности (x_n) действительных чисел и верхнюю грань значений, принимаемых этой последовательностью.

Рассмотрим последовательность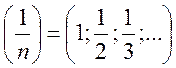

lim x_n = lim  = 0, однако sup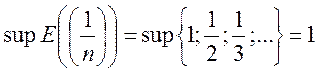

14.5  Лемма о предельной точке.

Как и в школе под ε-окрестностью точки x₀ÎR, где ε всегда больше 0, будем понимать интервал (x₀- ε, x₀+ ε).

Опредеение: Точка x₀ÎR называется предельной точкой числового множества X, если любая ее ε-окрестность содержит хотя бы одну точку xÎX и x≠x₀.

Элемент “+∞” является предельной точкой любого неограниченного сверху числового множества “-∞” – предельная точка любого неограниченного снизу числового множества.

Предельные точки могут как принадлежат, так и не принадлежать множеству.

Из определения вытекает, что предельная точка x₀ числового множества Х в любой своей окрестности содержит бесконечное множество точек, отличных от х₀.

Это позволяет дать равносильное.

Определние : Точка x₀ÎR называется предельной точкой числового множества Х, если любая ее ограниченность содержит бесконечно много точек Х.

Примеры:

1) 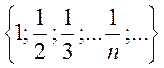единственная предельная точка 0

2) Х = (0;1] предельная точка – любая точка отрезка (0;1]

Множество Х, состоящее из конечного числа точек, не может иметь предельную точку.

Справедлива так назывемая,

Лемма (о предельной точке). Всякое бесконечно ограниченное числовое множество имеет, по крайней мере, одну предельную точку.

◄ По условию, Х ограниченно:

 $aÎR , $bÎR  "xÎX   рассмотрим .

Доказываем методом деления отрезка пополам. Через ∆₁ обозначим ту из его половинок, что содержит бесконечное множество точек Х и находится правее… По лемме о вложенных отрезков 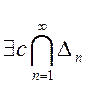, которая и будет предельной точкой множества Х►

Если х₀ – предельная точка Х, то $ последовательность (x_n) элементов Х, попарно различных которые сходятся к т. х₀.