Вписывание кривых в углы магистрального хода, страница 3

2 Σ Т_полн – Σ К_полн = Σ D_полн;

Σ К_полн + Σ Пр = L_тр.

3.2.4. Разбивка кривых без переходных кривых

Разбиваем круговую кривую на пикеты.

1. Вычисляем угол β, связывающий дугу от точки НЗ до точки первого полного пикета на кривой:

где s – длина дуги (расстояние от НЗ до полного пикета на круговой кривой).

2. Определяем координаты точки первого полного пикета на круговой кривой:

откладываем координату х от НЗ по линии тангенсов, у – перпендикулярно линии тангенсов.

3. Определяем местоположение следующего пикета для того, чтобы оценить длину хорды, стягивающей пикеты на кривой.

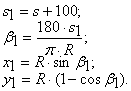
4. Створом циркуля разбиваем кривую дальше до ПК КЗ.

5. На втором отрезке ломаной от КЗ до ВУ2 с помощью линейки находим точку с полным пикетом и далее разбиваем отрезок на пикеты до ВУ2.

6 Задаем значение радиуса для второго угла поворота и вычисляем элементы кривой. В том случае, когда тангенсы двух кривых перекрываются – уменьшаем значения радиусов. Если значения радиусов достигли минимальных значений, а тангенсы все равно перекрываются, то необходимо изменить положение вершин ломаного хода (уменьшаем, например,  значения углов поворота или убираем лишние углы поворота).

Пример разбивки кривой без переходных кривых

s=400-337,08=62,92

   

6.

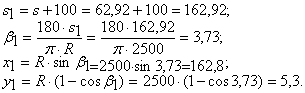
5.   

6.  Находим координаты точки НКК и ККК относительно НЗ и КЗ:

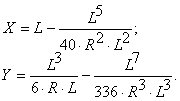
6. Разбивку пикетов на круговой кривой можно выполнить аналогичным случаю разбивки без переходных кривых. Только координаты вычисляются относительно точки НКК.

8. Оформление плана трассы.

Толщина линии трассы – 1-1,5 мм. Прямые участки от кривых отделяют пунктирными линиями внутрь кривой. Линии тангенсов показывают пунктирами. Каждому углу поворота присваивают номер. Все подписи, цифры пикетов пишут вдоль трассы перпендикулярно оси.

Параллельно оси трассы для каждого прямолинейного участка пишут в виде дроби его протяженность и румб. Например:

Пр. 1300 м

СВ 15°