Изучение затухающих электромагнитных колебаний с помощью электронного осциллографа (Лабораторная работа № 10)

Лабораторная работа 10

Изучение затухающих электромагнитных колебаний

с помощью электронного осциллографа

Цель работы: получение и наблюдение затухающих электромагнитных колебаний; ознакомление с основными количественными характеристиками колебательного контура.

Задание 1. Рассчитать период затухающих колебаний, коэффициенты затухания , логарифмические декременты затухания , добротность контура Q, время релаксации , число колебаний  при различных параметрах колебательного контура  и .

Приборы и принадлежности: низкочастотный осциллограф, магазин    емкостей, магазин сопротивлений, катушки индуктивности 50 мГн и 100 мГн или мост индуктивности.

Теория метода

Для возбуждения электромагнитных колебаний служат колебательные   RLC–контуры. Контур с сосредоточенными параметрами состоит из конденсатора С, катушки индуктивности L и проводов, обладающих электрическим сопротивлением R. В ходе колебательного процесса периодически меняются
(т. е. колеблются) заряд q на обкладках конденсатора C, напряжение на конденсаторе U_с и сила тока I, текущего через индуктивность L. Для цепи (рис. 1) закон Ома имеет вид

 + ℰ_L,                                                    (1)

где 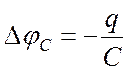; ℰ_L = ℰ_is .

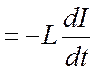	Подставив в (1) получим уравнение .                         (2) Разделив уравнение (2) на L, заменив  через , а  через , получим дифференциальное уравнение затухающих колебаний: .                       (3)
Рис. 1. Колебательный контур	Введя обозначения  и ,

уравнению (3) можно придать вид

.                                                  (4)

Уравнение (4) совпадает с дифференциальным уравнением затухающих механических колебаний.

При условии  решение уравнения (4) имеет вид

,                                               (5)

где

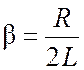 – коэффициент затухания;                                    (6)

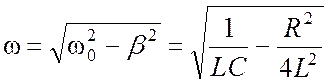 – круговая частота затухающих колебаний;        (7)

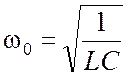 – круговая частота собственных колебаний;                  (8)

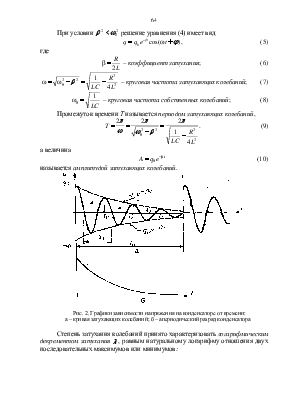
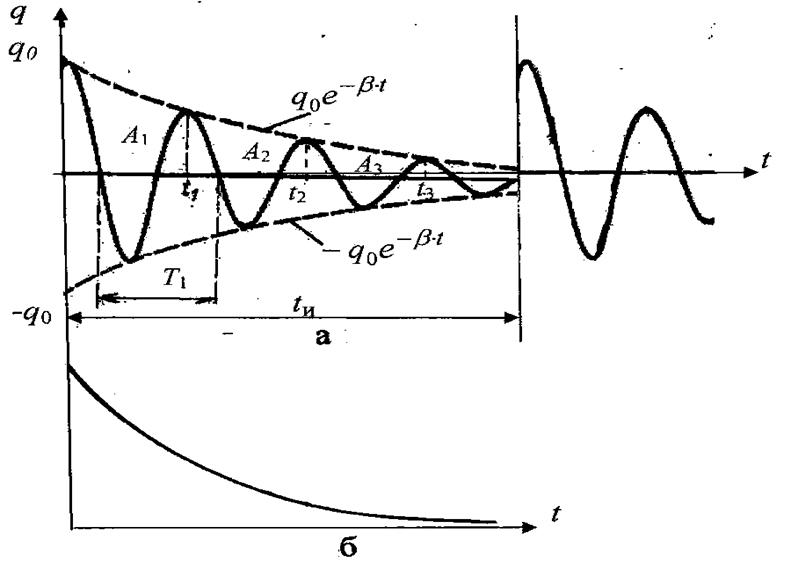
Промежуток времени Т называется периодом затухающих колебаний,

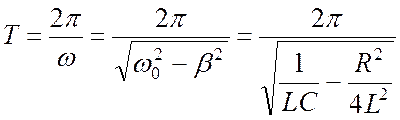.                                    (9)

а величина

                                                       (10)

называется амплитудой затухающих колебаний.

	Рис. 2. Графики зависимости напряжения на конденсаторе от времени: а – кривая затухающих колебаний; б – апериодический разряд конденсатора

 

Степень затухания колебаний принято характеризовать логарифмическим декрементом затухания , равным натуральному логарифму отношения двух последовательных максимумов или минимумов:

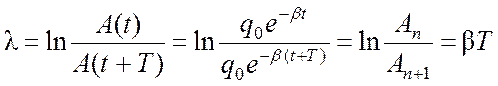,                             (11)

где n = 1, 2, …

Во многих случаях после убывания амплитуды колебаний в е раз можно считать, что колебания практически прекратились. Время убывания амплитуды в е раз называется временем релаксации :

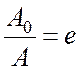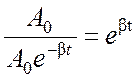; .                                              (12)

Следовательно,  = 1.

Исходя из (11) и (12), можно получить

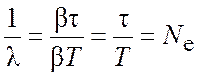,                                                 (13)

где  – число колебаний за время релаксации .

Для характеристики затухания колебательных контуров пользуются понятием добротность контура Q (в радиотехнике). Она связана с логарифмическим декрементом соотношением

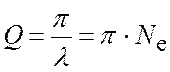.                                                   (14)

По (14) видно, что добротность контура тем выше, чем больше число колебаний успевает совершиться прежде, чем амплитуда уменьшится в е раз.

В случае слабого затухания

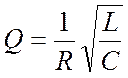.                                                       (15)

Описание установки и теория метода

Если в R-L-C контуре конденсатор однократно зарядить, отключить источник питания, предоставить контур самому себе, подключив конденсатор к входу Y осциллографа, то затухающие колебания в контуре быстро прекратятся, и на экране осциллографа мы не увидим устойчивой картины затухающих колебаний. Для получения устойчивой картины необходимо подавать на конденсатор кратковременные импульсы напряжения, частота которых больше 10 Гц. В данной работе вместо прямоугольных импульсов напряжения, питающего контур, можно брать прямоугольные импульсы, формируемые калибратором осциллографа, калиброванные по амплитуде и длительности, с частотой следования 1 000 Гц. Калибратор амплитуды и длительности служит для периодической поверки коэффициента отклонения луча и проверки калибровки длительности развертки осциллографа.

	Рис. 3. Электрическая схема лабораторной установки

 

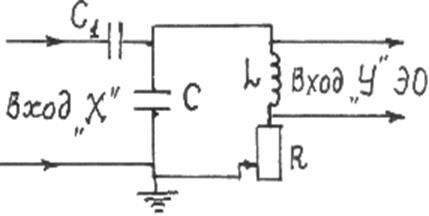
Принципиальная электрическая схема лабораторной установки изображена на рис. 3. Прямоугольный импульс напряжения поступает от калибратора на конденсатор С колебательного контура через разделительный конденсатор С₁. Зарядка конденсатора осуществляется практически мгновенно, поскольку сопротивление цепи заряда мало.

Затем конденсатор разряжается через сопротивление R и катушку индуктивностью L. Если R<R_кр, то в колебательном контуре возникают затухающие колебания. При прохождении следующего импульса процессы заряда и разряда повторяются. Напряжение с индуктивности колебательного контура поступает на вход Y электронного осциллографа ЭО. При включенной развертке на экране осциллографа можно наблюдать кривую затухающих колебаний (рис. 2, а).

Напряжение на конденсаторе меняется по закону

.                                                (16)

Напряжение на катушке L будет меняться по закону

,                                           (17)

отличающемуся от (16) только амплитудой и начальной фазой. Из формулы (6) видно, что, изменяя R и L, изменяем и коэффициент затухания.

Осциллограф универсальный С1-73

Осциллограф малогабаритный универсальный предназначен для исследования формы электрических сигналов в диапазоне частот от 0 до 5 МГц и измерения амплитуды в диапазоне от 0,02 до 120 В, с выносным делителем 1:10 до 350 В, временных интервалов от 0,2∙10^-6 до 0,5 с.