



Лабораторная работа 3
Изучение зависимости сопротивления металлов
от температуры
Цель работы: экспериментальное изучение зависимости сопротивления металлов от температуры и определение температурного коэффициента сопротивления.
Задание 1. Изучить зависимость сопротивления меди катушки от температуры
и определить температурный коэффициент сопротивления (ТКС) ![]() .
.
Приборы и принадлежности: катушка с обмоткой из медной проволоки, магазин сопротивлений МСР-63, источник постоянного тока, ключ замыкания.
Теория метода
Если проводник имеет форму проволоки круглого сечения, то зависимость его сопротивления от размеров наиболее проста
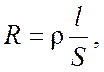 (1)
(1)
где l – длина проводника; S – его поперечное сечение; r – коэффициент пропорциональности, он называется удельным сопротивлением данного вещества проволоки.
Удельное
сопротивление r зависит не только от химического
состава вещества, но и от его состояния, в частности от температуры.
Электропроводность металлов 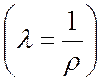 обусловлена дрейфом
электронов проводимости под действием приложенного извне электрического поля
обусловлена дрейфом
электронов проводимости под действием приложенного извне электрического поля ![]() . Поскольку в идеальной решетке электрон
может двигаться беспрепятственно, причиной сопротивления металла является
рассеяние электронов дефектами решетки. Эти дефекты можно разбить на два
класса: тепловое движение атомов, или фононов, и геометрические дефекты – вакансии, атомы в междоузлах, примесные атомы,
дефекты упаковки и поверхности. Предполагая, что тепловые и геометрические дефекты
рассеивают электроны независимо, можно представить удельное сопротивление
металла с малым количеством примеси в виде суммы двух слагаемых (правило Матиссена)
. Поскольку в идеальной решетке электрон
может двигаться беспрепятственно, причиной сопротивления металла является
рассеяние электронов дефектами решетки. Эти дефекты можно разбить на два
класса: тепловое движение атомов, или фононов, и геометрические дефекты – вакансии, атомы в междоузлах, примесные атомы,
дефекты упаковки и поверхности. Предполагая, что тепловые и геометрические дефекты
рассеивают электроны независимо, можно представить удельное сопротивление
металла с малым количеством примеси в виде суммы двух слагаемых (правило Матиссена)
![]() (2)
(2)
где rост – остаточное удельное сопротивление, не зависящее от Т и связанное с рассеиванием электронов на примесях и дефектах решетки; rид – идеальное сопротивление, зависящее от температуры и вызвано рассеиванием на фононах.
Таким образом, идеальное удельное сопротивление является характеристикой металла, а rост характеризует качество проводника.
Для большинства металлов при не слишком больших температурах сопротивление R меняется с температурой линейно
![]() ,
(3)
,
(3)
где
![]() – сопротивление при температуре
– сопротивление при температуре ![]() 0С;
0С; ![]() –
сопротивление при 0 0С;
–
сопротивление при 0 0С; ![]() – температурный коэффициент
сопротивления; t –
температура по шкале Цельсия (по шкале Кельвина зависимость имеет более простой
вид:
– температурный коэффициент
сопротивления; t –
температура по шкале Цельсия (по шкале Кельвина зависимость имеет более простой
вид: ![]() ).
).
При низких температурах наблюдается отступление от закономерности (3).
Температурный коэффициент сопротивления (ТКС) показывает изменение каждой единицы сопротивления при нагревании на один градус:
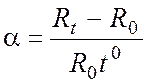 (град-1).
(4)
(град-1).
(4)
Для всех чистых металлов ![]() близок
к
близок
к 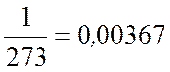 , т. е. к температурному коэффициенту
расширения газов. Для некоторых электротехнических сплавов (манганин, нихром,
константан)
, т. е. к температурному коэффициенту
расширения газов. Для некоторых электротехнических сплавов (манганин, нихром,
константан) ![]() настолько мал, что можно им пренебречь и
сопротивление считать не зависящим от температуры.
настолько мал, что можно им пренебречь и
сопротивление считать не зависящим от температуры.
Зависимость сопротивления металлов от температуры используют в различных измерительных и автоматических устройствах. Наиболее важным является термометр сопротивления. Он представляет собой сопротивление из платиновой проволоки (более чувствительны полупроводниковые сопротивления), которое включают в схему моста в качестве одного из плеч.
Из формулы (3) имеем
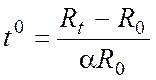 . (5)
. (5)
По закону Ома
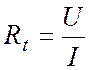 . (6)
. (6)
Преобразуем равенство (5)
![]()
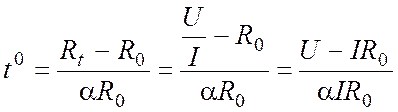 , (7)
, (7)
где
t0 –
температура проводника; U – разность потенциалов на концах проводника (или
напряжение); I –
ток; R0 –
сопротивление проводника при 0 0С;
![]() – температурный коэффициент сопротивления.
– температурный коэффициент сопротивления.
Описание установки
Сопротивление проводника Rx определяется при помощи линейного мостика постоянного тока (мостик Уитстона), схема которого дана на рис. 1.
Применим к контурам АСD и СВD второе правило Кирхгофа и получим
|
|
Так как ток в гальванометре отсутствует(нулевой метод), первое правило Кирхгофа к узлам С и D запишется в виде
По выражениям (8) и (9) получим
где |
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.