Измерение мощности, выделяемой в цепях переменного тока (Лабораторная работа № 12)

Лабораторная работа 12

Измерение мощности, выделяемой в цепях

переменного тока

Цель работы: измерение мощности переменного тока и сдвига фаз между током и напряжением на различных участках цепи.

Задание 1. Рассчитать , ,  при различных нагрузках.

Задание 2. Снять зависимость  и построить график этой    зависимости.

Приборыи принадлежности: ваттметр, амперметр (3 А) и вольтметр    (50 В) переменного тока, батарея конденсаторов, катушка индуктивности,    сердечник, ЛАТР.

Теория метода

Если через нагрузку, обладающую активным и реактивным сопротивлением, течет квазистационарный синусоидальный ток, то среднее значение      активной мощности, выделяемой этим током в нагрузке, определяется формулой: , где  и U – действующие значения силы тока в нагрузке и   напряжения на нагрузке; j – сдвиг фаз между током и напряжением на нагрузке.

В данной работе необходимо измерить активную мощность, поглощаемую различными нагрузками, и сдвиг фаз между током и напряжением. В качестве нагрузок (потребителей тока) используются: 1) реостат, 2) катушка индуктивности, 3) конденсатор, 4) последовательное соединение реостата, катушки индуктивности и конденсатора.

Рассмотрим кратко последовательное соединение R, L, С. Ток в цепи     изменяется по закону

.                                                     (1)

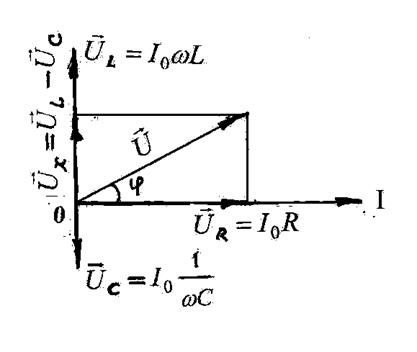
Вычислим напряжение между концами цепи (рис. 1). Искомое напряжение есть сумма

(2)

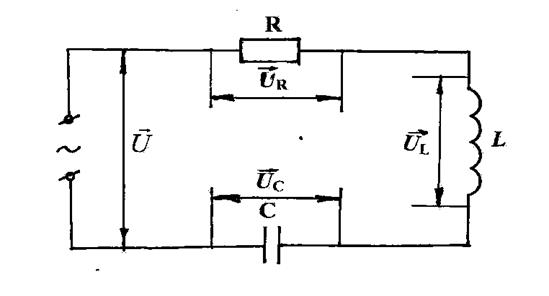
Рис. 1. Электрическая схема цепи

Для сложения этих напряжений воспользуемся векторной диаграммой напряжений (рис. 2). Изменение напряжения (колебания) на R изображаются вектором, направленным вдоль оси тока и длиной . Изменения же на  L и С – векторами, перпендикулярными к оси токов, с длинами  и 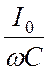. Складывая два последних слагаемых, мы получим одно гармоническое колебание 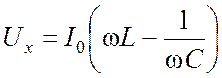, изображаемое вектором, перпендикулярным оси .

Ось тока

Рис. 2. Векторная диаграмма напряжений

Таким образом, полное напряжение U можно рассматривать как сумму двух гармонических колебаний: напряжения U_R, совпадающего по фазе с током, и напряжения U_х, отличающегося по фазе на .

U_R получило название активной составляющей напряжения; U_x – реактивной составляющей. Оба эти колебания, складываясь, дают также гармоническое колебание

,                                                (3)

где j – сдвиг фазы результирующего напряжения. Из треугольника напряжений (рис. 2) получаем

(8)

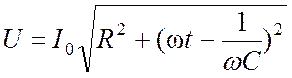.                                           (4)

Из рис. 2 видно, что

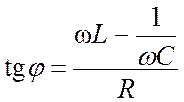.                                                  (5)

Формула (4) называется законом Ома для цепи переменного тока. Но эта формула относится только к амплитудным, а не к мгновенным значениям напряжения и тока.

Величину

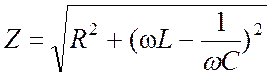                                           (6)

называют сопротивлением цепи для переменного тока (полным сопротивлением), где Х = Х_L – Х_C  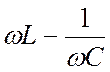=  – реактивное сопротивление цепи (реактанс). Наличие реактивного сопротивления не сопровождается выделением тепла (это – кажущееся сопротивление).

Вычислим мощность переменного тока. Мгновенная мощность переменного тока .

Необходимо знать мощность тока за большой период времени, охватывающий много периодов колебаний (изменений тока), т. е. нужно вычислить среднее значение мощности за один полный период Т. Работа тока за малое время dt есть , а за время Т → .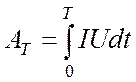

Так как напряжение U складывается из двух слагаемых U_R и U_х, то

.

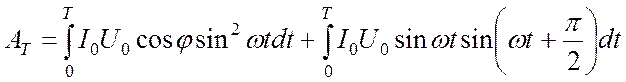Нетрудно заметить, что одно из них, обусловленное реактивной составляющей напряжения, равно нулю. Следовательно, полная работа за время Т   определяется только активной составляющей напряжения

.

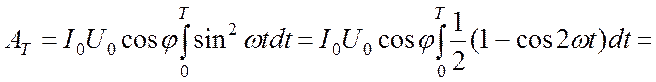
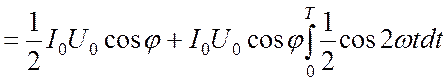Но .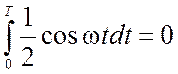

Отсюда 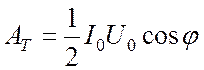, а средняя мощность переменного тока равна

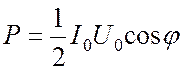.                                                 (7)

Полученное выражение имеет дополнительный множитель cosj, называемый в электротехнике коэффициентом мощности. Это показывает, что в общем случае выделяемая в цепи мощность зависит не только от силы тока и напряжения, но и от сдвига фазы, определяемой по (5).

Если активное сопротивление в цепи R = 0, то tgj = ¥ и 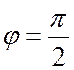. В этом случае в цепи мощность не выделяется, так как cosj = 0. Мощность будет    максимальной при условии, что Х = Х_L – Х_С = 0 и равна 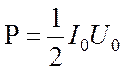. Эту формулу можно записать через эффективные значения тока  и напряжения U_эф. Приборы в цепи измеряют обычно эффективные значения 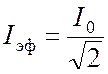, 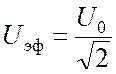. Тогда мощность переменного тока определяется выражением P = _эф·U_эф.

Пользуясь эффективными значениями, можно, следовательно, выразить среднюю мощность переменного тока формулой