1. Постановка задачи
Разработать программу построения по данным заданной таблицы прямой линии регрессии и интерполяционного полинома Лагранжа.
Результаты работы программы представить в виде значений параметров прямой, вычисленных методом наименьших квадратов, и таблицы расчетных значений для данных исходной таблицы. Кроме того, предусмотреть возможность диалога программы с внешним пользователем для расчета значений функции регрессии и полинома Лагранжа по введенному значению аргумента.
|
Х |
1 |
3 |
6 |
7 |
2 |
4 |
12 |
15 |
5 |
9 |
|
Y |
50 |
175 |
180 |
200 |
60 |
140 |
420 |
540 |
170 |
300 |
2. Описание интерфейса программы
При запуске программы на экран выводится значения исходной таблицы, значения параметров a и b,посчитанных методом наименьших квадратов. Выводится новая таблица значений функции, которая подсчитана с помощью подставления х в уравнение линии регрессии (х подставляется из исходной таблицы). Затем программа запрашивает новое значение аргумента (не из таблицы) и подсчитывает значение функции с помощью уравнения линии регрессии и полинома Лагранжа.
3. Описание алгоритмов решения задачи
Вычисление коэффициентов a и b в уравнении линии регрессии по формулам:
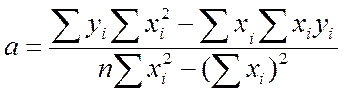 ,
,
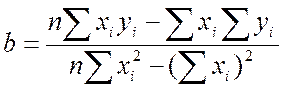 ,
,
i, n – от 1 до 10
значение линии регрессии вычисляется по формуле:
y=a+bx,
значение интерполяционного полинома Лагранжа вычисляется по формуле:
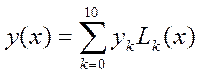 ,
,
где
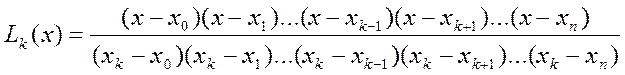 .
.
Значение аргумента х, вводится с клавиатуры.
4. Текст программы
#include<iostream>
using namespace std;
void main()
{
int x[10]={1,3,6,7,2,4,12,15,5,9},//64
y[10]={50,175,180,200,60,140,420,540,170,300},
n(10),i,j;//2235
double y_new[10],a,b,c,d,x1(0),y1(0),x2(0),xy(0),
ch(0),y_end(0),x_end(0);
//Вывод начальных векторов x и y
cout<<" Ha4a/|bHbIe DaHHbIe: "<<endl<<"x = ";
for (i=0;i<10;i++)
cout<<x[i]<<" ";
cout<<endl<<"y = ";
for (i=0;i<10;i++)
cout<<y[i]<<" ";
cout<<endl;
//промежуточный рассчет сумм xi,xi^2,yi,xi*yi
for (i=0;i<10;i++)
{
x1+=x[i];
x2+=x[i]*x[i];
y1+=y[i];
xy+=x[i]*y[i];
}
//Рассчет a и b
a=(y1*x2-x1*xy)/(n*x2-x1*x1);
cout<<"a = "<<a<<endl;
b=(n*xy-x1*y1)/(n*x2-x1*x1);
cout<<"b = "<<b<<endl;
//Рассчет нового вектора y(y_new)
cout<<"HoBbIe y: "<<endl;
for (i=0;i<9;i++)
{
y_new[i]=a+b*x[i];
cout<<y_new[i]<<" ";
}
cout<<endl;
//Просчет новых y
cout<<" XoTuTe IIoc4uTaTb y, IIpu HoBoM x???"<<endl<<
" IIPuwJIu sms Ha HoMeP 3434 s IIoMeTKou Xo4y"<<endl;
cin>>ch;
if (ch==1)
{
cout<<" BBeDuTe X.."<<endl;
cin>>x_end;
cout<<" MaJIoBaT Pa3MeP4uK..)"<<endl;
y_end=a+b*x_end;
cout<<"y=a+b*x; y="<<y_end<<endl;
for (int k=0; k<10; k++)
{
c=1;
d=1;
for(i=0;i<10;i++)
if (i!=k)
c=(x_end-x[i]);
for(j=0;j<10;j++)
if (j!=k)
d*=(x[k]-x[j]);
y_end+=(y[k]*c/d);
}
cout<<" 3Ha4eHue uHTePIIoJI9c,uoHHoro IIoJIuHoMa:"<<endl;
cout<<y_end<<endl;
}
system("pause");
}
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.