Отчёт
По лабораторной №4
“Вещественная арифметика”
Работу выполнил
Студент гр. 4561 Иванова Н.Д.
1. Постановка задачи
Написать на языке C++ функции вычисления числа p двумя способами.
1-ый способ – статистический (число p вычисляется по формуле: 4Sкр./Sкв., где Sкв. и Sкр. – площади ¼ квадрата со стороной 1 и ¼ круга вписанного в этот квадрат соответственно. А площади Sкв и Sкр определяются по количеству точек с координатами в интервале [0;1] , попадающим в них).
2-ой способ – геометрический (число p равно половине длины окружности единичного радиуса. Длина этой полуокружности определяется путём определения длины ломаной вписанной в неё).
Сравнить результаты вычислений.
2. Описание входных и выходных параметров. Оператор прототипа
Для 1 – ой функции:
Оператор прототипа: double statist(long h)
Входные данные:
h – количество проверяемых точек.
Функция возвращает значение числа p.
Для 2 – ой функции:
Оператор прототипа: double geom ( double e)
Входные данные:
e–погрешность вычислений.
Функция возвращает значение числа p.
3. Описание алгоритма
1-ая функция:
С помощью функции rand() получаем координаты точек в интервале [0;1]. Очевидно, что все они попадут в четверть квадрата. Подставляя координаты точек в неравенство: x2+y2<=1 выясняем попадают ли точки в четверть круга. Вычисляем число p.
2-ая функция:
Беря начальное значение длины ломаной, вписанной в полуокружность, равным 2 (2 радиуса), вычисляем длины ломанных, полученных при дальнейшем разбиении по формуле:
![]() =
=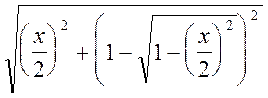
Проделываем это до тех пор пока разность между длинами звеньев ломаной в данном и предыдущем вычислении не станет меньше погрешности. По полученным результатам вычисляем число p.
4. Текст программы
#include <math.h>
#include <stdlib.h>
#include <time.h.>
double sqr(double a)
{
a=a*a;
return a;
}
double statist(long h)
{
srand(time(NULL));
int d=0;
for (int g=1;g<=h;g++)
{
int u=rand();
double i=double(u);
double x=i/RAND_MAX;
int v=rand();
double j=double(v);
double y=j/RAND_MAX;
if ((sqr(x)+sqr(y))<=1) d++;
}
double d1=double(d);
double h1=double(h);
double r=4*d1/h1;
return r;
}
double geom ( double e)
{
double x;
double m;
int t=1;
m=e+1;
double x0=2;
while (m>e)
{
x=sqrt(sqr(x0/2)+sqr(1-sqrt(1-sqr(x0/2))));
m=t*x0-t*2*x;
x0=x;
t*=2;
}
x=x*t;
return x;
}
void main()
{
double pi1=geom(0.00001);
double pi2=statist(1000000);
}
5. Анализ результатов и вывод
Для нахождения числа p болееэффективен геометрический способ. При нахождении числа p этим способом получается наиболее точное значение, чем при вычислении статистическим способом.
Для функции находящей число p статистическим способом:
Если число проверяемых точек равно n, то программа выполнит :
2n вызовов функции rand();
4n операций преобразования типов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.