Построение множественного уравнения регрессии зависимости цены от 3 характеристик (качества звучания, оснащения, объема памяти) устройств. Анализ исходных данных, страница 2

 Итоговое уравнение Y ⁽ⁱ⁾=a₁*X ⁽ⁱ⁾ ₄+a₂*X ⁽ⁱ⁾ _{5  ,}  выглядит как

Y ⁽ⁱ⁾ = 0,631*X ⁽ⁱ⁾ ₅  

 5.2. Стандартный (метод наименьших квадратов).

 Результаты составной регрессии

 Подчиненный фактор цена,$

 Умножение R   0,71074021

  F = 16,33314                 (коэффициент Фишера)

  R?=  0,50515165

  df =   3,48

 Число случаев:52 

adjusted R?=  0,474223

p =  0,000000

 Standard error of estimate:  0,725104389

 Разрыв:      0,000000000  Std.Error: 0,1005539  t(48) = 0,00000  p = 1,0000

                                                                               

  качество звучания beta=0,102     оснащение beta=0,281 объем памяти, beta=0,563    

Итоговое уравнение выглядит как

Y ⁽ⁱ⁾ =0,102* X ⁽ⁱ⁾ ₃ +0,281 *X ⁽ⁱ⁾ ₄+0,563*X ⁽ⁱ⁾ ₅ 

 

Но так как в модели присутствует незначимый фактор, то такая модель является пригодной для анализа, но не пригодной для прогнозирования.

6.проверка значимости коэффициентов регрессии на основе t-критерия Стьюдента

Красным цветом подсвечены значимые коэффициенты, таким образом В (разрыв) является не значимым и соответственно в уравнении а₀ равен 0.

В обоих случаях (и для объема памяти и для оснащения) вероятность p меньше чем 0,05,следовательно, эти коэффициенты включаются в модель.

7. проверка значимости уравнения регрессии по F-критерию Фишера-Снедекера

Проведем проверку адекватности всей модели с помощью критерия Фишера-Снедекера и величины средней ошибки аппроксимации, величина средней ошибки аппроксимации не должна превышать 12-15%.

Для принятия решения и проведения прогноза необходимо, чтобы построенная модель была адекватна по Фишеру, и каждый коэффициент регрессии был статистически значим по критерию Стьюдента с уровнем значимости L.

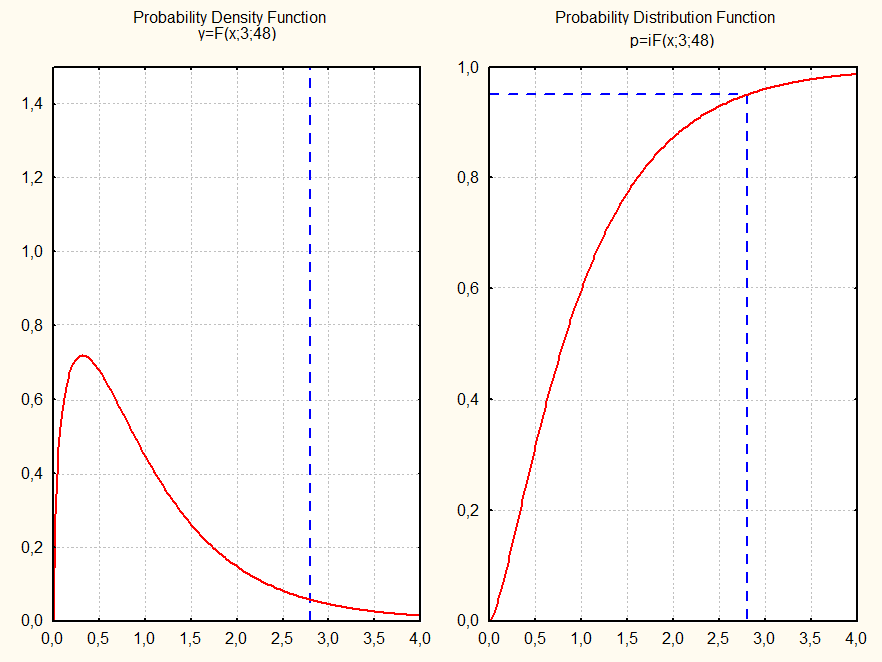
Критическое значение коэффициента Фишера F(0,05 ,3,48) равно 2,79.

Значения коэффициентов Фишера F ,полученные в результате методов пошаговой регрессии и VYR превышает критическое значение, следовательно, гипотеза о незначимости множественного коэффициента корреляции отвергается с уровнем ошибки 5%.

Проведем остаточный анализ.

Получим гистограмму остатков (для метода пошаговой регрессии вперед).

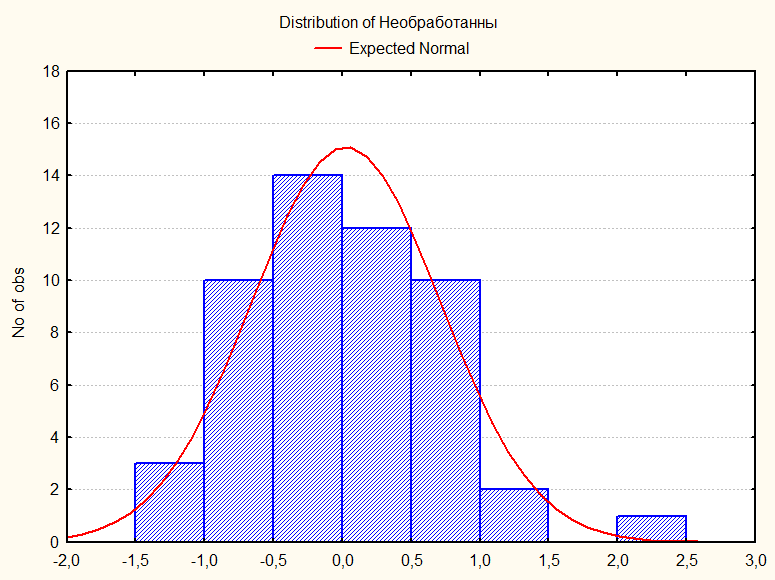
Получим гистограмму остатков (для метода пошаговой регрессии назад).

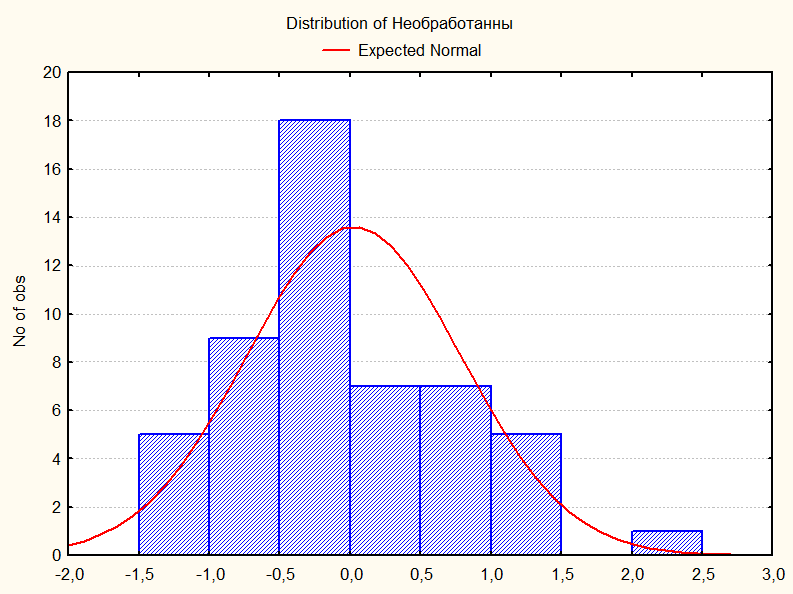
Получим гистограмму остатков (для метода МНК.)

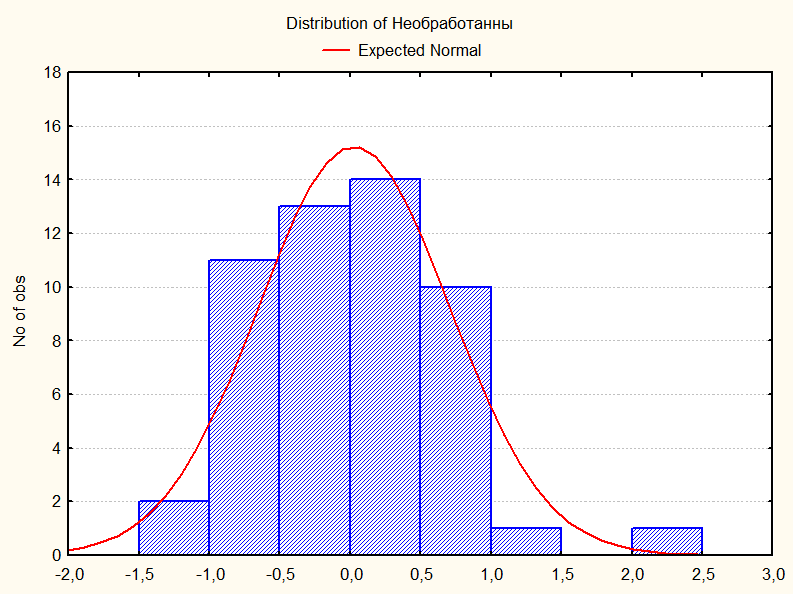
Получим нормальное вычерчивание остатков.

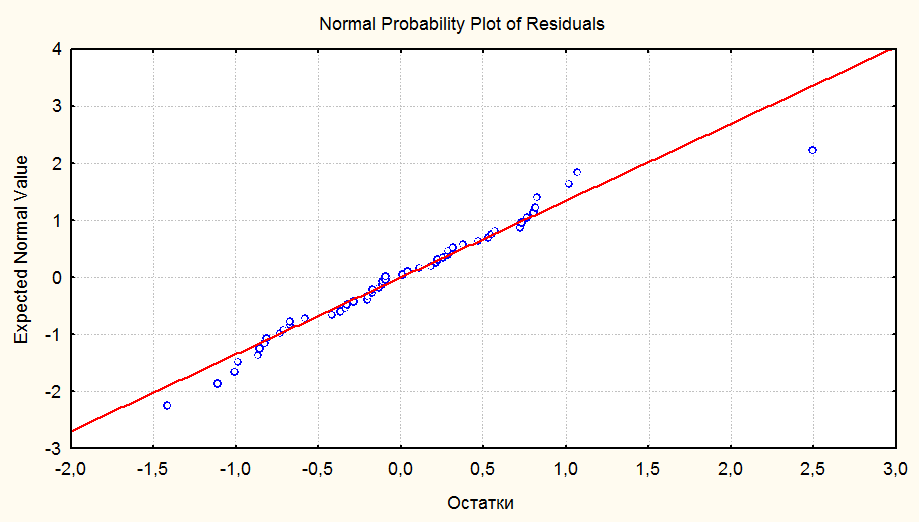
Для метода пошаговой регрессии (вперед пошагово).

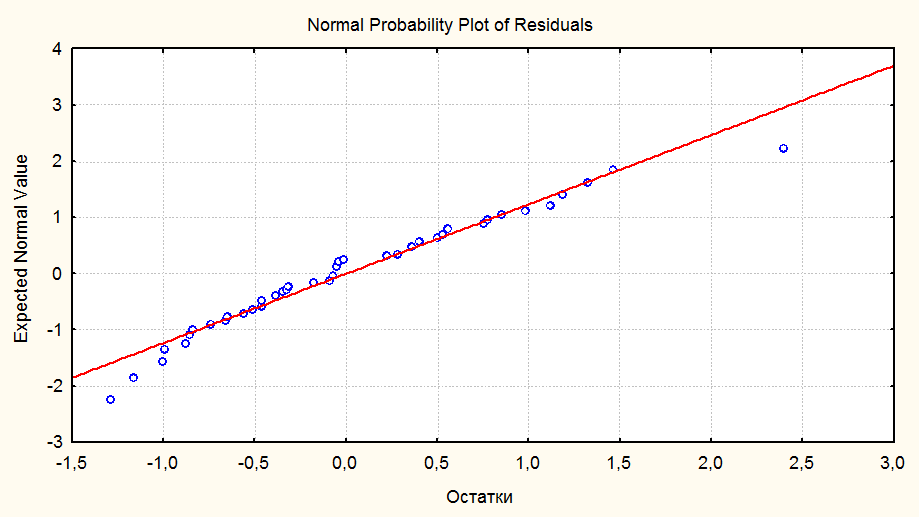
Для метода пошаговой регрессии (назад пошагово).

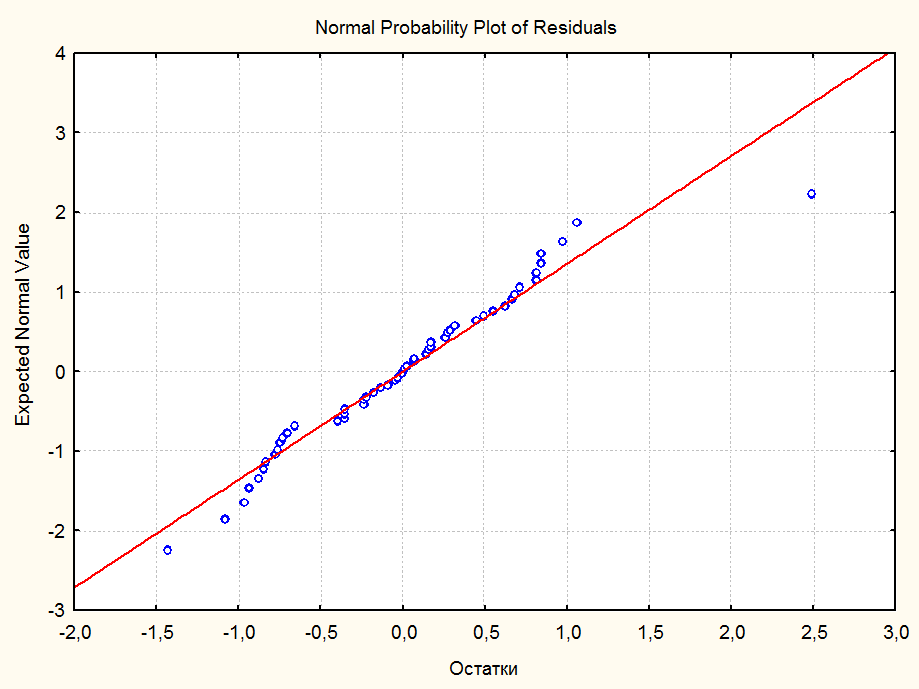
Для метода МНК.

8.статистически значимое уравнение регрессии, содержащее статистически значимые параметры

В ходе проведенных исследований получено три множественных уравнения регрессии зависимости цены от трех факторных признаков: качества звучания, оснащения и  объема памяти.

Y ⁽ⁱ⁾=a₁*X ⁽ⁱ⁾ ₃+a₂*X ⁽ⁱ⁾ ₄ +a₃*X ⁽ⁱ⁾ _{5   ,}

 

 

(1) Y ⁽ⁱ⁾ = 0, 328*X ⁽ⁱ⁾ ₄+0, 538*X ⁽ⁱ⁾ ₅ 

(2) Y ⁽ⁱ⁾ = 0,631*X ⁽ⁱ⁾ ₅ 

(3) Y ⁽ⁱ⁾ =0,102* X ⁽ⁱ⁾ ₃ +0,281 *X ⁽ⁱ⁾ ₄+0,563*X ⁽ⁱ⁾ ₅ 

 

Для дальнейшего анализа и прогнозирования наиболее подходящим является уравнение (1),полученное методом пошаговой регрессии вперед, так как все коэффициенты в нем значимы, оно отражает зависимость цены от двух значимых факторов: оснащения и объема памяти.

Коэффициент детерминации R? характеризует, какая доля вариации результата обусловлена изменением факторных признаков, входящих в многофакторную модель. В идеале коэффициент детерминации должен стремиться к 1, поэтому, сравнивая результаты, полученные методами пошаговой регрессии, мы выбираем тот результат, где  значение R? больше, таким образом, нами выбран метод пошаговой регрессии вперед.

В третьем уравнении значение R? еще больше, но оно непригодно, для дальнейшего прогнозирования из-за незначимых факторов.

 

9.экономическая интерпретация коэффициентов уравнения регрессии

Для прогноза мы используем табличную модель, она является наглядной и удобной в пользовании.

Коэффициент разрыва равен 0 ,следовательно, при нулевых значения факторных признаков, значение зависимого признака равно 0.

Оба коэффициента положительны.