Лабораторная работа №2
1. Построить множественное уравнение регрессии зависимости цены от 3 характеристик (качества звучания, оснащения, объема памяти).
2. Анализ исходных данных производить согласно «Схемы построения множественного уравнения регрессии» (см. конспект лекций).
3. 
Построение уравнения производить, используя пошаговую регрессию вперед. Выбрать
модель регрессии для проведения прогноза. Сделайте выводы.
Порядок выполнения работы:
Построим множественное уравнение регрессии зависимости цены от 3 характеристик (качества звучания, оснащения, объема памяти).
Необходимо получить уравнение вида y=a0+a1*x3+a2*x4+a3*x5 ,где x3, x4, x5 - факторные признаки, а a0 - свободный коэффициент, а a1… a3 соответственно коэффициенты уравнения регрессии, которые и надо вычислить.
 |
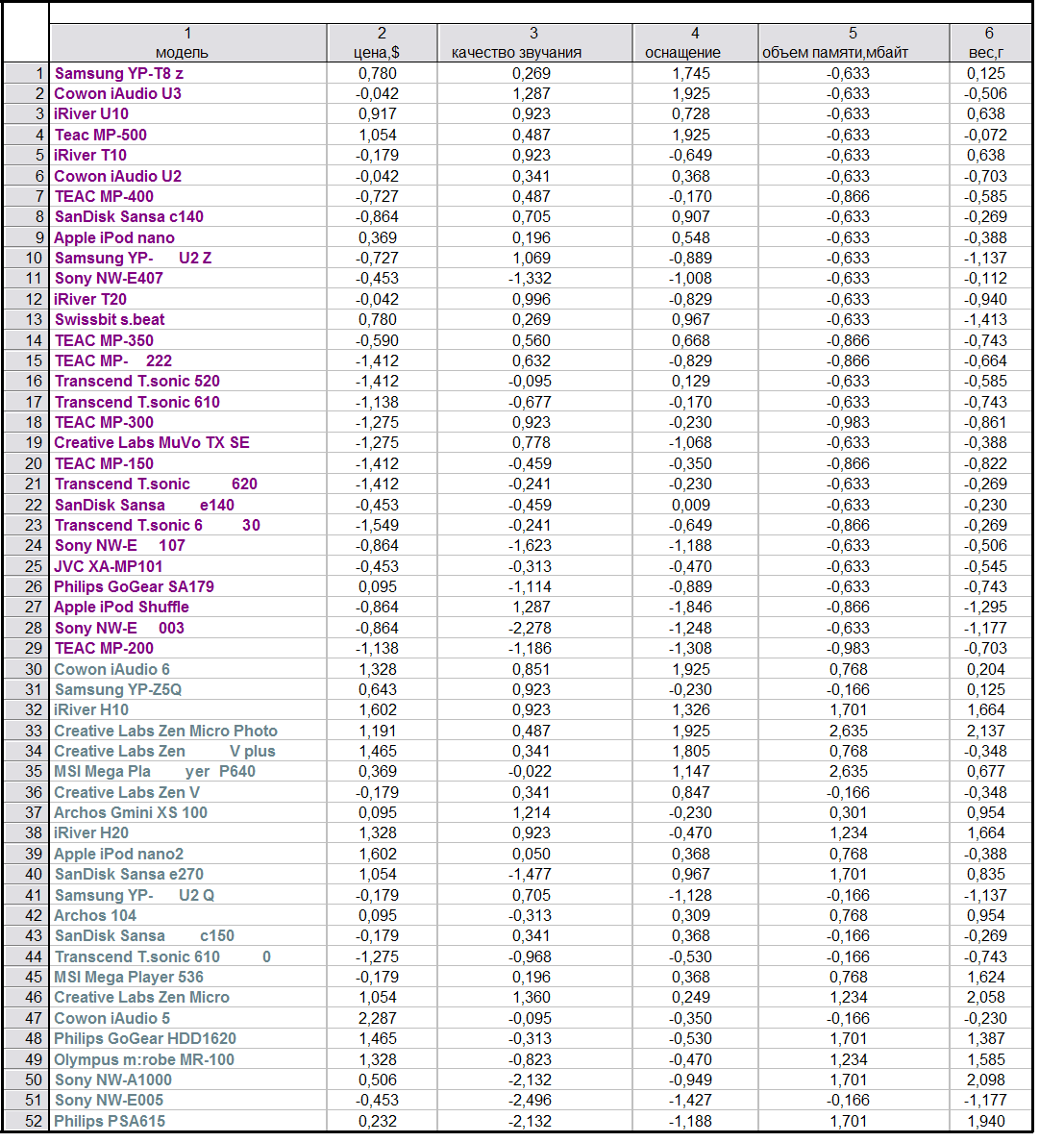
1.матрица исходных данных

Данные стандартизованы, так как имеют различные единицы измерения.
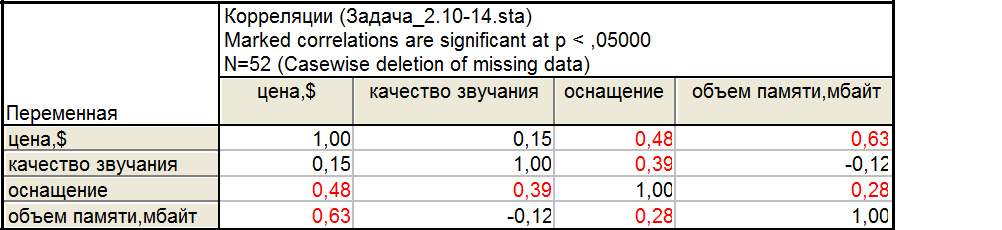
2.матрица парных коэффициентов корреляции
3.проверка значимости парных коэффициентов корреляции на основе t-критерия
Зависимость результативного признака «Цена» от признака X (i) 3

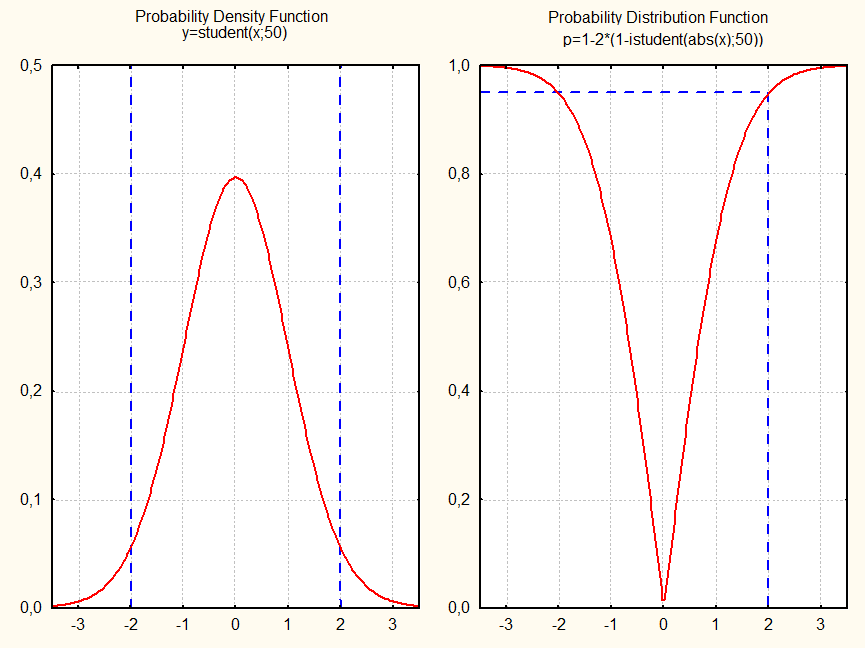
t наблюдаемое (1,0436) меньше t критического 2,009. Следовательно,
гипотезу о статистически незначимом отличии от 0 выборочного парного коэффициента корреляции нужно принять.
Зависимость результативного признака «Цена» от признака X (i) 4

t наблюдаемое (3,8782) больше t критического 2,009. Следовательно,
гипотезу о статистически незначимом отличии от 0 выборочного парного коэффициента корреляции нужно отклонить.
Зависимость результативного признака «Цена» от признака X (i) 5

t наблюдаемое (5,749) больше t критического 2,009. Следовательно,
гипотезу о статистически незначимом отличии от 0 выборочного парного коэффициента корреляции нужно отклонить.
Красным подсвечены значимые коэффициенты, то есть, нет ни одного факторного признака в модели, который бы имел значимую связь со всеми другими признаками.
Зависимость цены от оснащения и объема памяти более сильная, чем от качества звучания, эти факторные признаки значимы и их мы включаем в множественное уравнение регрессии.
4.анализ матрицы парных коэффициентов корреляции на наличие мультиколлинеарности
Индикатором наличия мультиколлинеарности является превышение парного линейного коэффициента по модулю 0,8.
Из матрицы (2) очевидно, что ни один из парных линейных коэффициентов корреляции не превышает 0,8.
5.построение уравнения многофакторной регрессии
5.1. пошаговый регрессионный анализ
5.2. МНК
В модель многофакторной регрессии включаем только 2 признака - оснащение и объем памяти.
5.1.1.Пошаговый регрессионный анализ «вперед пошагово».
Результаты составной регрессии (step 2, final solution)
no other F to enter exceeds specified limit
подчиненный фактор цена,$
Умножение R 0,70497034
F = 24,20613 (коэффициент Фишера)
R?= 0,49698318
df = 2,49
Число случаев:52
adjusted R?= 0,47645188
p = 0,000000
Standard error of estimate: 0,723566251
Разрыв: 0,000000000 Std.Error: 0,1003406 t(49) = ,00000 p = 1,0000
объем памяти, beta=0,538 оснащение beta=0,328

Итоговое уравнение Y (i)=a1*X (i) 4+a2*X (i) 5 , выглядит как
Y (i) = 0,3282*X (i) 4+0,5376*X (i) 5
5.1.2.Пошаговый регрессионный анализ «назад пошагово».
Результаты составной регрессии(step 2, final solution)
no other F to remove is less than specified limit
подчиненныйцена,$
Умножение R 0,63083931
F = 33,05072 (коэффициент Фишера)
R?= 0,39795824
df = 1,50
Число случаев:52
adjusted R?= 0,38591740
p = 0,000001
Standard error of estimate: 0,783634225
Разрыв: 0,000000000 Std.Error: 0,1086705 t(50) = 0,00000 p = 1,0000
объем памяти, beta=0,631

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.