Модель временного ряда. Прогноз будущих значений временного ряда на 3 значения и построение доверительного интервала прогноза с уровнем доверия 0.9

Задача 4

Требуется:

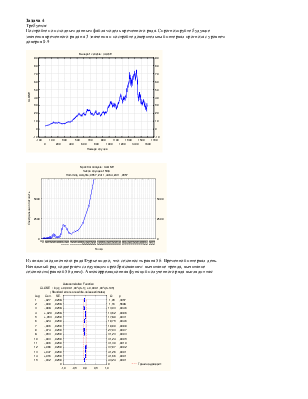
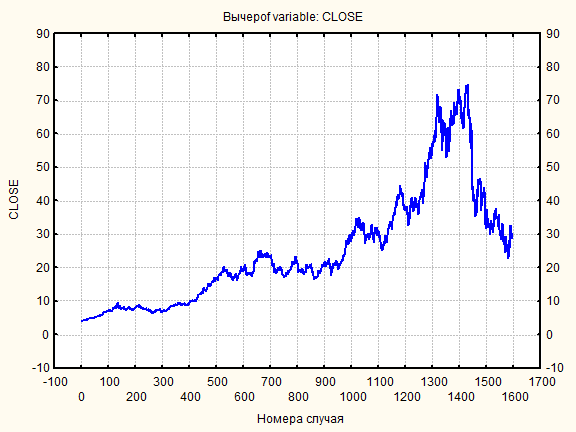
Постройте по исходным данным файла модель временного ряда. Спрогнозируйте будущие значения временного ряда на 3 значения и постройте доверительный интервал прогноза с уровнем доверия 0.9

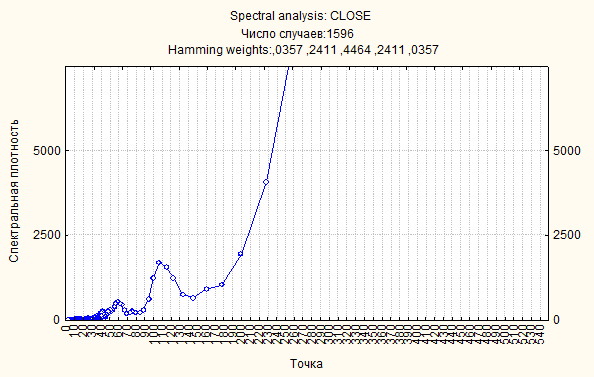
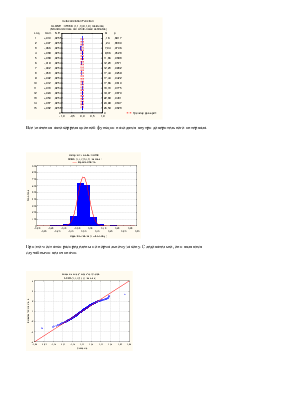
Из анализа одиночного ряда Фурье видно, что сезонность равна 56. Временной интервал день.

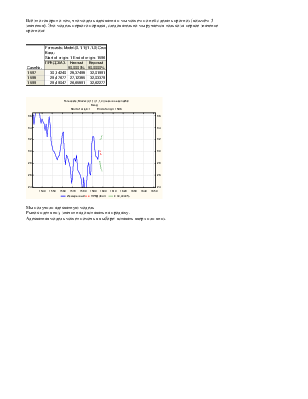
Начальный ряд подвергаем следующим преобразованиям: вычитание тренда, вычитание сезонности(равной 56 дням). Автокорреляционная функций полученного ряда выглядит так:

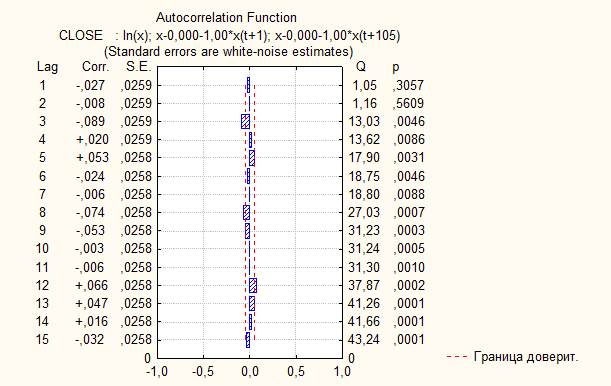
Виден выброс на третьем шаге, следовательно процесс не случайный.

Получаем модель уже преобразованного ряда (за минусом тренда и сезонности):

        Variable: CLOSE   

 Transformations: ln(x),D(1),D(56)

           Model: (0,1,1)(1,1,0)  Seasonal lag: 56

 No. of obs.:  1539    Initial SS= 2,6424 Final SS= 2,0717(78,40%)  MS= ,00135

  Parameters (p/Ps-Autoregressive, q/Qs-Moving aver.); highlight: p<.05

              q(1)  Ps(1)

   Оценка:   ,05375 -,4796

   Std.Err.: ,02619 ,02305

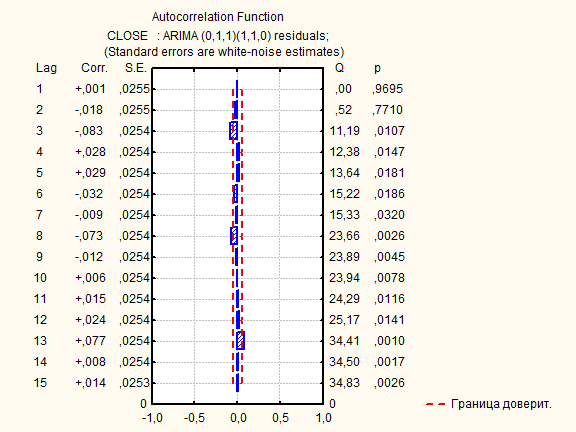
Однако видно, что на 3,8 и 13 шаге значение автокорреляционной функции остатков выходит за пределы доверительного интервала. Следовательно, эта модель для прогноза не годится.

Получим ещё одну модель:

     Variable: CLOSE   

 Transformations: ln(x),D(1),D(56)

           Model: (1,1,1)(0,1,0)

 No. of obs.:  1539    Initial SS= 2,6424 Final SS= 2,6321(99,61%)  MS= ,00171

  Parameters (p/Ps-Autoregressive, q/Qs-Moving aver.); highlight: p<.05

              p(1)   q(1)

   Оценка:   ,69088 ,73613

   Std.Err.: ,13803 ,12857

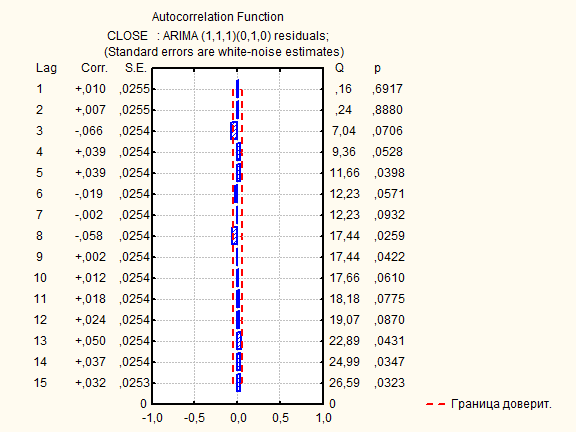
Все значения автокорреляционной функции находятся внутри доверительного интервала.

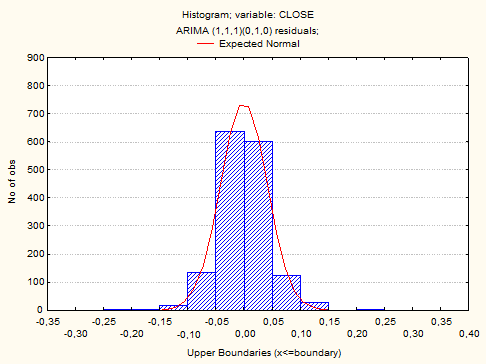
При этом остатки распределены по нормальному закону. Следовательно, они являются случайными величинами.

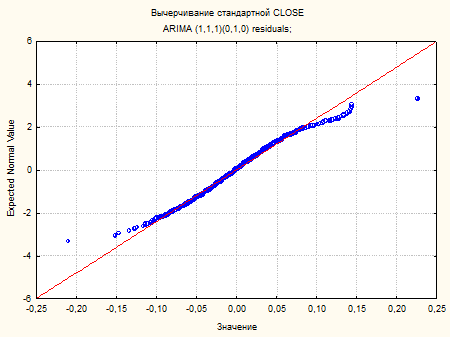
Всё это говорит о том, что модель адекватна и мы можем по ней сделать прогноз (возьмём 3 значения). Это модель первого порядка, следовательно мы ручаемся только за первое значение прогноза:

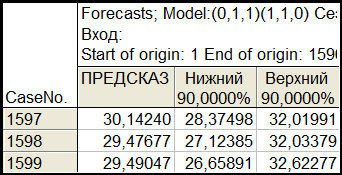
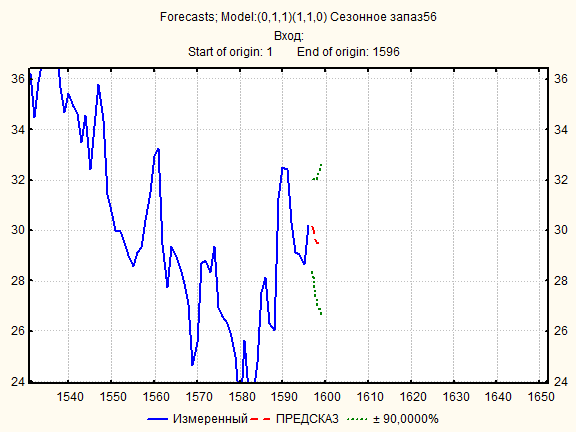
Мы получили адекватную модель

Рынок идет вниз, значит надо вставать на продажу.

Адекватная модель может помочь в выборе: вставать вверх или вниз.