Моделирование процессов сетями Петри

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ СЕТЯМИ ПЕТРИ

Возникновение теории сетей Петри было обусловлено развитием научно-технического прогресса, а именно появлением возможности построения многопроцессорных систем. Модели параллельных процессов, отражающих одновременную работу нескольких устройств, потребовали создания новых способов их отображения. Теория сетей Петри разработана немецким математиком Карлом-Адамом Петри в диссертационной работе «Взаимодействующие автоматы» в 1962г. Сети Петри получили широкое распространение, так как позволили объединить работу нескольких устройств, описываемых отдельными связанными автоматами.

Сетью Петри называется ориентированный двудольный (бихроматический) граф G_p=(P, T, K, S), в котором P и T – два множества вершин, причем P={p_i} – множество вершин позиций p_i, T={t_j} – множество вершин переходов t_j (PÇT = Æ), соединенных между собой дугами K = P´TÈT´P по функциональным правилам S.

В общем случае функциональные правила S включают матрицы инциденций и ингибиторных дуг, вектора (функции) начальной маркировки, временных задержек и приоритетов переходов.

В зависимости от функциональных правил S формируется требуемая интерпретация сетей Петри, обусловливающая ее конкретное применение.

Способы задания сетей Петри

Можно указать три эквивалентных способа задания сетей Петри:

-  графический;

-  аналитический;

-  матричный.

Графический способ

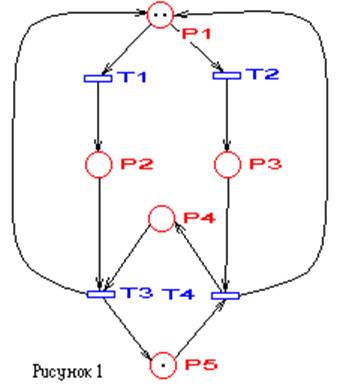
Как показано на рис.1, множество элементов P графа Петри G_p, часто обозначаемого PN, изображаются кружками, а множество T – утолщенными короткими прямыми линиями. Множество дуг, которое соответствует множествам упорядоченных пар вершин (p_i, t_j) и (t_j, p_i) называют множеством дуг K графа PN.

Графическое изображение вершин переходов также может быть представлено в виде квадратов или прямоугольников.

Логические условия процесса задаются правилами движения маркеров через переходы:

1.  Если к переходу T_j подходит более одной дуги, то он  открывается  после выполнения последней операции в позициях, из которых к нему подходят дуги.

2.  Дуга может иметь кратность, соответствующую числу  проходящих  через нее маркеров. Переход разрешен, если число маркеров во входной позиции не меньше кратности дуги из  этой позиции.

3.  Если к переходу подходит несколько дуг, а выходит одна дуга, то несколько маркеров сливаются в один. Если к переходу  подходит  одна дуга, а выходят несколько дуг, то после перехода один маркер делится на несколько по числу дуг.

4.  Переходы могут иметь разные приоритеты (pr). В  этом  случае маркер сначала движется через переход с более высоким приоритетом.

5.  Ингибиторная дуга (с кружком вместо стрелки)  запрещает открывание  перехода  T_j, если в позиции, откуда она выходит, имеется маркер.

Маркеры и переходы могут иметь разную  окраску.  При  этом маркеры определенного цвета могут двигаться через переходы такого же цвета.

Аналитический способ

Говорят, что задана сеть Петри PN = (P, T, K, S), если заданы множества P, T, K и отображение S : ((P´T) È (T´P)) ®K(1).

Часто отображение S несет не только указанную функцию, но и включает правила соединения вершин между собой и правила, отражающие обход ветвей сети при практической реализации PN. Если число вершин p_i и t_j конечно, то сеть Петри называется конечной, в противном случае – бесконечной.

Пусть заданны конечные множества P = {p₁, p₂, ..., p_n}и T = {t₁, t₂, ..., t_k}. Из определения сетей Петри и функциональных правил S следует, что Q = P´TиR = T´P, тогда выражение (1) можно представить в виде: S : (QÈR) ®K.

Здесь множества Q иR для каждых пар вершин (p_i, t_j) и (t_j, p_i) включают соответственно подмножества дуг K^Op_i Î Q или K^It_j Î Q и K^Ip_j Î Rили K^Ot_j Î R(O – output, I – input). Подмножество дуг (p_i, t_j), выходящих из вершины p_i, обозначается K^Op_i, а входящих в t_j – K^It_j. Подмножество дуг (t_j, p_i), выходящих из вершины t_j, обозначается K^Ot_j, а входящих в p_i - K^Ip_j.

Часто возникает необходимость указания всех вершин t(p), входящих в вершину p_i(t_j) или выходящих из вершины p_i(t_j). Подмножество T^Op_i включает все вершины t_n, к которым направлены дуги из K^Op_i от вершины p_i, а подмножество T^Ip_i содержит все вершины t_m (t_m, t_n Î T), от которых дуги из K^Ip_j направлены к вершине p_i. Аналогично подмножества P^It_j содержат все вершины p_k, дуги от которых из K^It_j направлены к t_j, а подмножество P^Ot_j – все вершины p_l, дуги к которым из K^Ot_j направлены от t_j (p_k, p_l Î P).

Матричный способ

Структура  сети задается матрицей инциденций, элементами которой являются числа

Aij =

|   К,  если дуга К-й кратности выходит из |   перехода Tj и выходит в позицию Pi; | - К,  если дуга К-й кратности выходит из |   позиции Pi и входит в позицию Tj; |   0, если Tj и Pi не соединены дугой.

Параметры технологического процесса задаются вектором исходного распределения маркеров по n позициям сети    

         Мо  =  ( P1, P2, P3, ..., Pn ),

где

Pi =	|  0, когда в Pi нет маркера; | |  1, когда в Pi есть маркер;

вектором задержек Z_i маркеров в позициях  (временем  выполнения операций):

         Mz  =  ( Z1, Z2, Z3, ..., Zn ),

вектором  приоритетов переходов 

        Mpr = (pr 1,pr 2,pr 3,...,pr n),

где pr i - приоритет соответствующего перехода;

и матрицей ингибиторных дуг ING_i,j из элементов:

INGi,j =

| 1, если дуга между позицией Pi и |    переходом Tj - ингибиторная; | | 0, если дуга между позицией Pi и |    переходом Tj - неингибиторная;

Таким образом, если сеть Петри задана одним из описанных выше способов (графическим, аналитическим или матричным), можно перейти к любому другому способу задания, а результаты, полученные с помощью одного, можно интерпретировать для другого. Наиболее часто сети Петри задаются графическим способом, отражая наглядность, полноту и однозначность решаемой задачи. При исследованиях сетей Петри с помощью ЭВМ используют аналитический или матричный способ задания.