Модели класса ARIMA (Лабораторная работа № 7), страница 3

          9. Диалог  ARIMA.  Теперь  надо  вернуться  к  диалогу  Single Series ARIMA  (Единственный  ряд  ARIMA),  нажав  кнопку    Cancel  (Отменить)  в  окне  TransformationsofVariables  (Преобразования  переменных).  В  окне  Single Series ARIMA  (Единственный  ряд  ARIMA)  выделить  исходную  переменную  Series_G.  Этот  диалог  позволит  определить  параметры  авторегрессии  и  скользящего  среднего  (сезонное  и  несезонное).  Нельзя  перейти  к  следующему  шагу  до  тех  пор,  пока  один  из  параметров  не  будет  выбран  (p, P, q или Q).  Однако  вначале  нужно  определить  преобразования  и  дифференцирования  (разности).  При  выделенной  опции  Quick (Быстрая)  в  окне  Transformvariable (series) priortoanalysis  (Преобразование  переменной (ряда)  для  анализа)  отметить  позиции   NaturalLog   (Натуральный  логарифм) и  Difference (Разность).  Теперь  укажем  в  окнах  1. Lag  =1   и   N. Ofpasses  =1,  что  определяет  логарифмическое  преобразование  и  несезонную  простую  разность.  Для  определения  сезонности  укажем  в  окнах  2. Lag   лаг= 12   и  N. of passes =1  (рис.10).

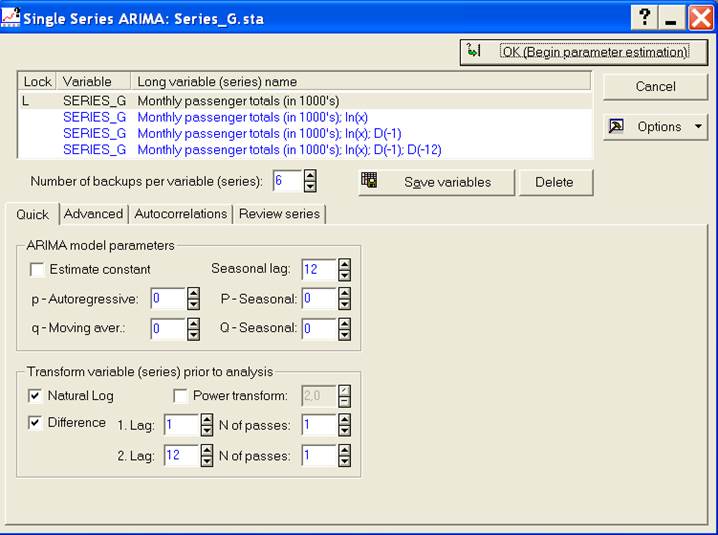
Рис.10. Диалоговое  окно  ARIMA

         10. Параметры  ARIMA.  На  стадии  идентификации  было  решено  оценить  2  параметра  скользящего  среднего:  один  регулярный  q и  один  сезонный  Q.  В  окне  параметров  надо  установить  значения  q=1  и  Q=1,  после  чего  нажать  ОК.

После  процесса  оценивания  параметров  в  окне  SingleSeriesARIMAResults  (Результаты)  появятся  результаты  расчета  (рис.11). 

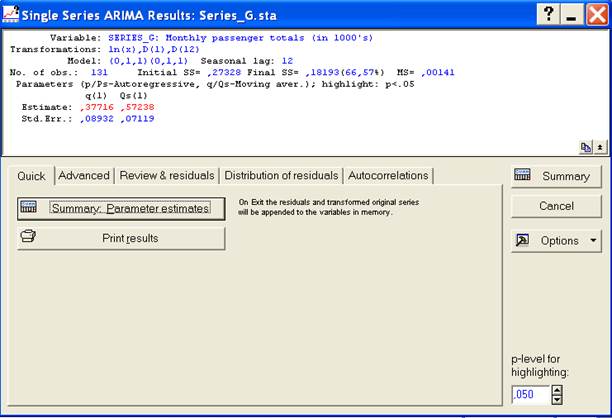
Рис.11. Окно  результатов  расчета

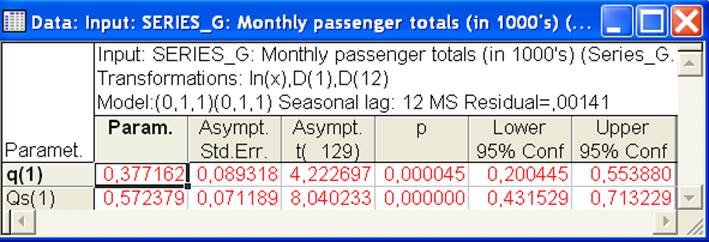
Итог  приведен  в верхней  части  окна  (модель,  преобразования).  После  нажатия  кнопки  Summary: Parameterestimates  (Итоги:  оценки  параметров)  появится  таблица  результатов   (табл.1),   откуда  видно,  что  параметры  скользящего  среднего  (сезонный  и  несезонный)  являются  высоко  значимыми.

Таблица 1. Результаты расчетов

11. Фаза  прогнозирования.  При  выделенной  опции  Advanced  (Расширенная)  появляется  окно Forecasting (Прогнозирование).  По  умолчанию  этот  пакет  будет  вычислять  прогнозы,  начиная  с  последнего  наблюдения   на  один  полный  сезонный  цикл  (на  12  месяцев,  начиная с  момента  времени,  равного  145).   Вначале  рассмотрим  прогнозы  в таблице,  нажав  кнопку  Forecastcases (Прогнозы).   Затем  можно  проанализировать  график  прогноза,  нажав  кнопку   Plotseries & forecasts  (График  ряда  и  прогноза)  (рис.12). Здесь  можно  также  рассмотреть,  как  ведет  себя  модель  прогноза  на  реальных  данных,  поставив  в  окне  начала  прогноза   цифру 133  (145-12+1=133).

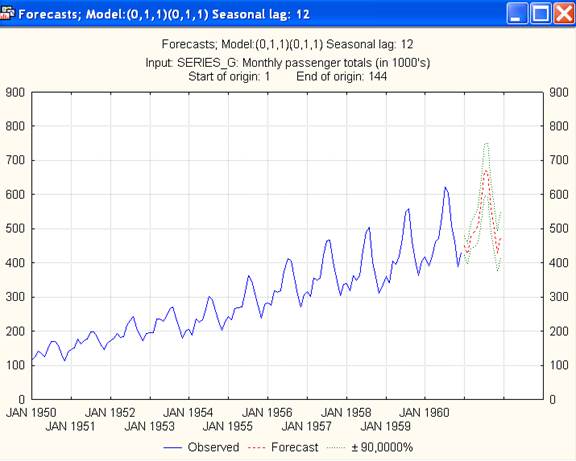
Рис.12. График  прогноза

12.Анализ   остатков.  Для  модели  ARIMA устанавливаются  два  допущения  об  остатках:

- остатки должны  быть  нормально  распределены;

- остатки должны  быть  независимы друг  от  друга  (отсутствует  остаточная  последовательная корреляция).

Первое  допущение  может  быть  проверено  рассмотрением  графика  нормального  распределения  остатков. При  выделенной  опции  Distributionofresiduals  (Распределение  остатков)  нажать  клавишу  Normal probabilityplots(Нормальные графики).  Если  остатки  нормально  распределены,  то  все  точки должны  группироваться  около  прямой  линии  на  графике  (рис.13).

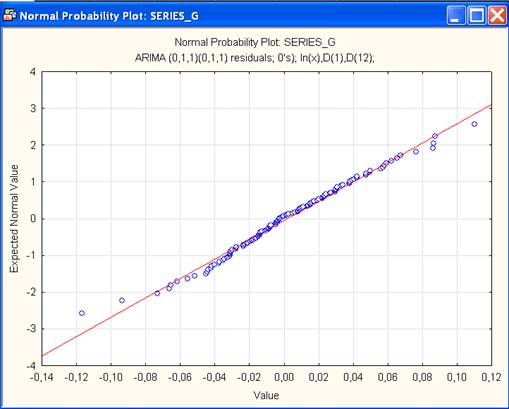
Рис.13. График  нормального  распределения  остатков

Второе  допущение  проверяется  с  помощью  вычисления автокорреляционной  функции:  при  выделенной  опции  Autocorrelations (Автокорреляции)  нажать  кнопку  Autocorrelations (Автокорреляции)  (рис.14).

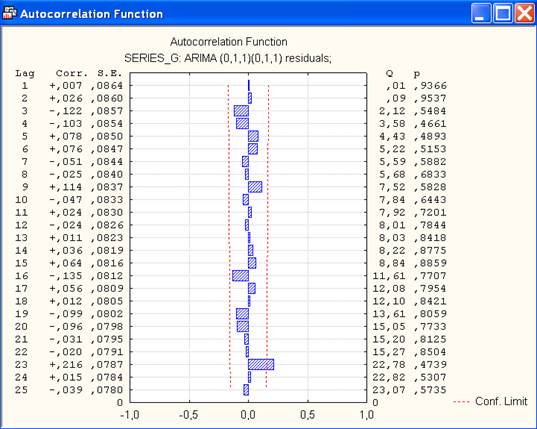
Рис.14. График  автокорреляций  остатков

         Из графика  видно,  что автокорреляция  остатков  практически отсутствует, следовательно,  условие  независимости  остатков  выполнено  для  выбранной  модели.

Задание

Построить  смоделированный  временной  ряд   в  пакете  Statistica   следующим  образом:

·  Создать  новый  файл,  состоящий  из  100  строк  и  1  столбца.

·  Через  меню  Data – VariableSpecs   (Данные – описание  переменной) ввести  в  окно  формул  выражение  =vnormal(rnd(1);1;3).

·   Смоделировать  100  значений  случайной  нормально  распределенной  величины    с  математическим  ожиданием,  равным  1,  и  среднеквадратичным  отклонением,  равным  3.  Эти  100  значений  определяют переменную  Var1. Перевести  их  к  целому  типу  данных,  установив  в  окне описания  переменной  в  качестве  Type   значение  Integer.

·  Провести  прогнозирование  полученного  ряда  с  помощью  подбора  модели  класса  ARIMA.