5. Автокорреляции. Выделить опцию Autocorrs (Автокорреляции) и изменить в окне Autocorrelations & crosscorrelations (Автокорреляции и кросскорреляции) параметр Numberoflags (Число лагов) с 15 на 25. Затем нажать клавишу Autocorrelations (Автокорреляции) для отображения таблицы и графика автокорреляционной функции (рис.7). График показывает сильную последовательную зависимость для лагов от 1 до 12 с максимальной величиной автокорреляции при лаге, равном 1.
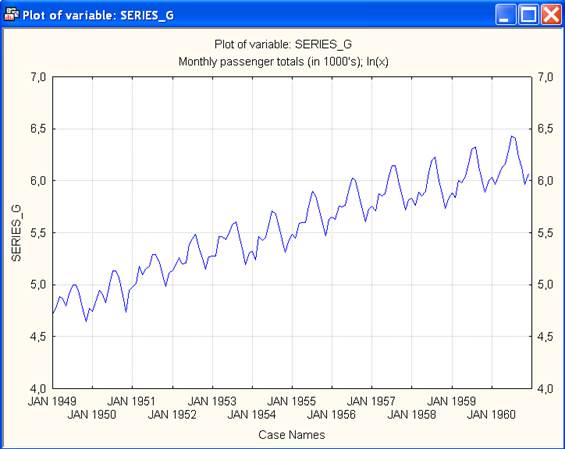
Рис.6. Трансформированный временной ряд
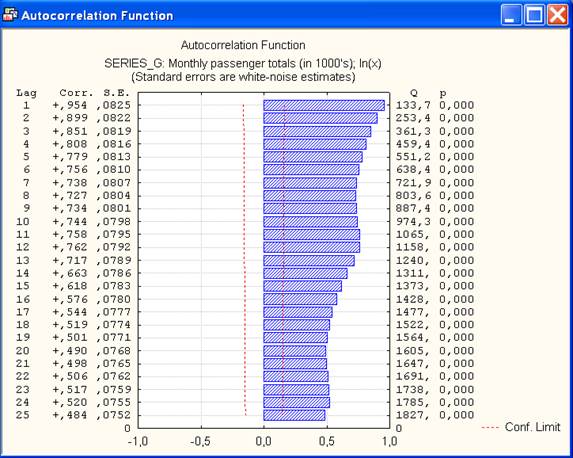
Рис.7. График автокорреляционной функции
6. Дифференцирование. Для устранения последовательной зависимости вначале необходимо выполнить дифференцирование ряда с лагом 1. (Отметим, что преобразованный (логарифмированный) ряд автоматически высветился в активной рабочей области.) Выделив опцию Difference, integrate (Дифференцирование, интегрирование), следует указать преобразование Differencing (x=x-x(lag)) и нажать ОК (Transformselectedseries) (Преобразование выделенного ряда). После выполнения преобразований на экране вновь появится преобразованный временной ряд (рис.8).
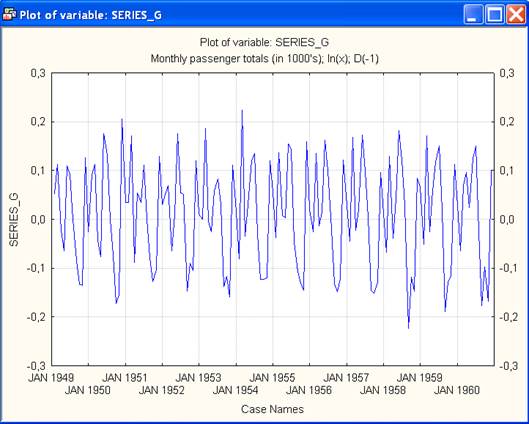
Рис.8. Преобразованный временной ряд
Теперь каждый элемент преобразованного ряда представляет разность между своим предыдущим и последующим значениями. При этом ряд стал короче на число элементов, равное лагу, т.е. 1, так как первый элемент ряда не участвует в этой операции.
Далее необходимо вернуться к диалогу TransformationsofVariables (Преобразования переменных), выделить опцию Autocorrs (Автокорреляции) и нажать кнопку Autocorrelations (Автокорреляции). Как видно из графика (рис.9), теперь не только зависимости первого порядка исчезли, но и большинство других зависимостей также стало достаточно малым.
7. Сезонная последовательная зависимость. Как видно из графика, устранение зависимостей низкого порядка показало, что проявляются зависимости высокого порядка (с лагом 12). Здесь наблюдается явная сезонная зависимость с лагами, равными 24, 36 и т.д., что отражает сезонность авиаперевозок. Дифференцирование с лагом 12 позволит устранить сезонность. Для этого необходимо вернуться к опции Difference, integrate (Дифференцирование, интегрирование), выбрать преобразование
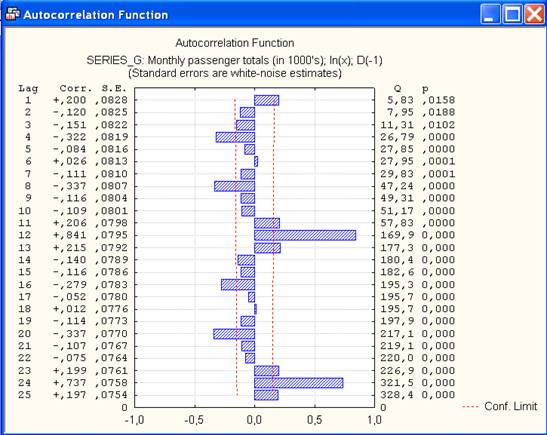
Рис.9. График автокорреляционной функции после преобразований
Differencing (x=x-x(lag)), но с измененным лагом, равным 12, и нажать ОК (Transformselectedseries) (Преобразование выделенного ряда). Как и прежде, появится график нового временного ряда. Теперь нажать кнопку Partialautocorrelations (Частные автокорреляции) и просмотреть график.
8. Оцениваемые параметры. Коррелограмма не показывает значимых выбросов, поэтому ряд готов для подбора модели. Основываясь на природе ряда, выбираем модель ARIMA с сезонностью, определяемой лагом = 12, и несезонностью с лагом=1. Таким образом, здесь нужно оценить 2 параметра модели скользящего среднего: сезонный (Q) и несезонный (q). Никаких параметров авторегрессии в данном случае не оценивается.
Модифицированный ряд теперь может быть подставлен непосредственно в модель ARIMA. Однако в случаях, подобных рассматриваемому, рекомендуется проанализировать исходный ряд и выбрать необходимые модификации данных как часть спецификаций модели. Вследствие этого ARIMA будет «знать» о модификациях, поэтому при необходимости прогнозирования оценки прогноза будут вычисляться из проинтегрированных (обратных дифференцированию) и ремодифицированных (обратных преобразованию) данных. Такие прогнозные оценки оказываются простыми для интерпретации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.