Эти два шага алгоритма иллюстрирует табл.3 для уже рассмотренного случая кодирования восьми символов.
Шаг 3. Строится кодовое дерево и, в соответствии с ним, формируются кодовые слова, соответствующие кодируемым символам.
Поясним принципы выполнения последнего шага алгоритма. Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщений по строкам и столбцам таблицы. Для наглядности строится кодовое дерево (рис.1). Из точки, соответствующей вероятности 1, направляются две ветви. Ветви с большей вероятностью присваивается символ 1, а с меньшей – символ 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до каждого символа.
Таким образом, символам источника сопоставляются концевые вершины дерева. Кодовые слова, соответствующие символам, определяются путями из начального узла дерева к концевым. Каждому ответвлению влево соответствует символ 1 в результирующем коде, а вправо – символ 0.
Поскольку только концевым вершинам кодового дерева сопоставляются кодовые слова, то ни одно кодовое слово не будет началом другого. Тем самым гарантируется возможность разбиения последовательности кодовых слов на отдельные кодовые слова.
 |
Рис.1. Кодовое дерево
Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
|
01 |
00 |
111 |
110 |
100 |
1011 |
10101 |
10100 |
Покажем, что использованный алгоритм позволяет однозначно декодировать полученное сообщение.
Пусть передаваемое сообщение a1,a5,a3,a7,a8. В результате кодирования по алгоритму Хаффмана получим следующую кодовую последовательность:
011001111010110100.
При приеме неизвестно, каким образом эту последовательность надо разбить на кодовые слова и, соответственно, получить последовательность переданных символов.
Просматриваем принятую последовательность слева направо, учитывая, что наибольшая длина кодового слова равна 5. Из первых пяти принятых элементов следует, что комбинация 01100 не встречается ни в одном кодовом слове. Единственным правильным решением будет, что первым был передан символ a1. Аналогично, продолжая просмотр с третьего слева элемента, определяем второй символ - a5. Аналогично декодируем все сообщение - .a1,a5,a3,a7,a8.
Таким образом, в передаваемой последовательности нет необходимости указывать разделители между отдельными кодовыми словами.
2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Исходными данными для данной лабораторной работы являются результаты статистической обработки текста. Выполненной в предыдущей лабораторной работе. ( см. лабораторную работу «Определение количества информации, содержащегося в сообщении». Из этой работы для заданного текста должны быть вычислены:
1. Оценка вероятностей появления символов в тексте;
2. Энтропия источника.
1. Построить код Шеннона-Фано для посимвольного кодирования заданного текста.
2. Построить код Хаффмана для посимвольного кодирования заданного текста.
3. Определить энтропию исреднее количество двоичных разрядов, необходимых для передачи текста при использовании эффективных кодов по п/п 2 и 3.
4. Проверит возможность однозначного декодирования полученных кодов, рассмотрев пример передачи слова, состоящего из 6-10 символов.
Примечание: расчеты рекомендуется выполнять в табличной форме, используя MS Excel.
3. СОДЕРЖАНИЕ ОТЧЕТА
3.1. Таблицы кодирование по алгоритмам Шеннона-Фано и Хаффмана.
3.2. Расчеты энтропии и среднего количества двоичных разрядов, необходимых для передачи текста при использовании эффективных кодов.
3.3. Результаты проверки возможности однозначного декодирования полученных кодов.
3.4. Выводы по работе.
Литература:
1. Савельев А.Я. Основы информатики: Учеб. Для вузов.- М.: Изд-во МГТУ им. Н.Э.Баумана, 2001.- 328 с.
2. Темников Ф.Е. и др. Теоретические основы информационной техники.- М.: Энергия, 1979.- 512 с.
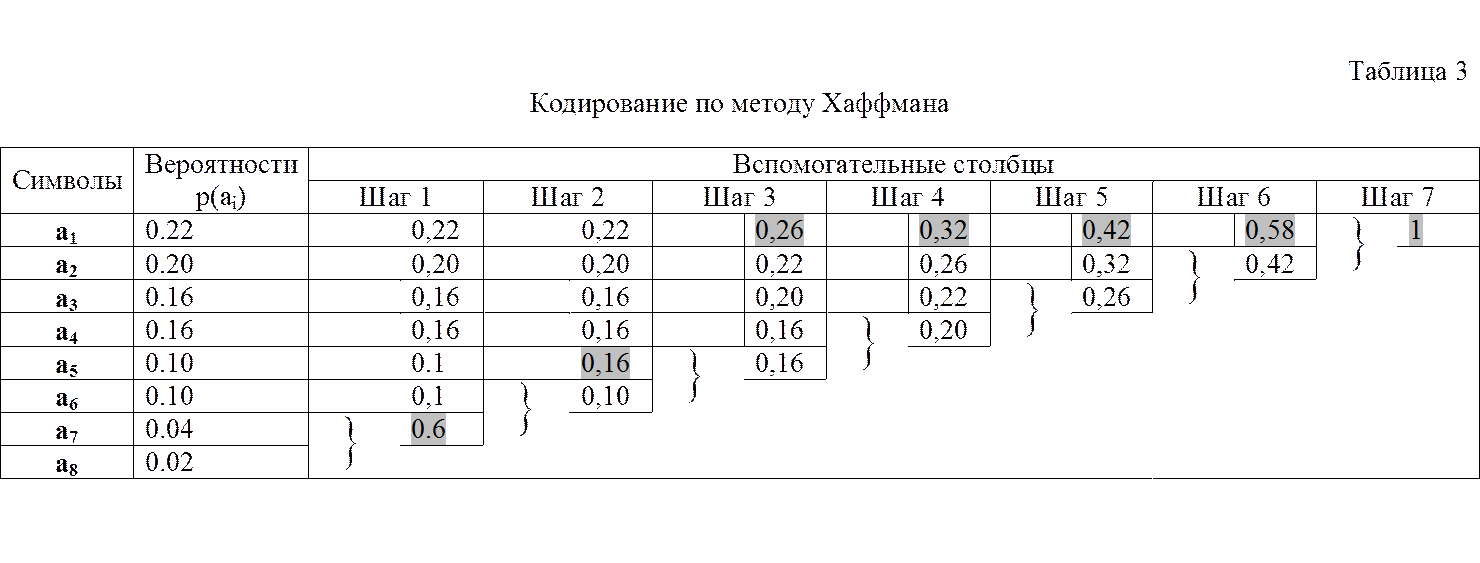
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.