Исследование методов эффективного кодирования дискретных источников информации (Лабораторная работа № 5), страница 2

Рассмотрим алфавит из восьми букв (табл. 1). Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется n₂ =3 символа. В табл.1 приведен один из возможных вариантов кодирования по сформулированному выше правилу.

Таблица 1
Символы	Вероятности p(ai)	Кодовые комбинации	1 ступень	2 ступень	3 ступень	4 ступень	5 ступень
a1	0.22	11
a2	0.20	10
a3	0.16	011
a4	0.16	010
a5	0.10	001
a6	0.10	0001
a7	0.04	00001
a8	0.02	00000

Очевидно, для указанных вероятностей можно выбрать другое разбиение на подмножества не нарушая алгоритма Шеннона-Фано. Такой пример приведен в табл.2.

Сравнивая приведенные таблицы, обратим внимание на то, что по эффективности полученные коды различны. Действительно, в табл.2 менее вероятный символ a₄ будет закодирован двухразрядным двоичным числом, в то время как a₂ , вероятность появления которого в сообщении выше, кодируется трехразрядным числом.

Таким образом, рассмотренный алгоритм Шеннона-Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппу.

Таблица 2
Символы	Вероятности p(ai)	Кодовые комбинации	1 ступень	2 ступень	3 ступень	4 ступень	5 ступень
a1	0.22	11
a2	0.20	101
a3	0.16	100
a4	0.16	01
a5	0.10	001
a6	0.10	0001
a7	0.04	00001
a8	0.02	00000

Энтропия набора символов в рассматриваемом случае определяется как

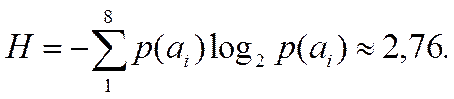
Напомним, что смысл энтропии в данном случае, как следует из теоремы Шеннона, – наименьшее возможное среднее количество двоичных разрядов, необходимых для кодирования символов алфавита размера восемь с известными вероятностями появления символов в сообщении.

Мы можем вычислить среднее количество двоичных разрядов, используемых при кодировании символов по алгоритму Шеннона-Фано

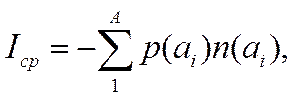                                                                (1)

где:

A–размер (или объем) алфавита, используемого для передачи сообщения;

n(a_i) – число двоичных разрядов в кодовой комбинации, соответствующей символуa_i.

Таким образом, мы получим для табл.1 I_ср=2,84, а для табл.2 I_ср=2,80. Построенный код  весьма близок к наилучшему эффективному коду по Шеннону, но не является оптимальным. Должен существовать некоторый алгоритм позволяющий выполнить большее сжатие сообщения.

От недостатка рассмотренного алгоритма свободна методика Д. Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом двоичных разрядов на символ.

Для двоичного кода алгоритм Хаффмана сводится к следующему:

Шаг 1. Символы алфавита, составляющего сообщение, выписываются в основной столбец в порядке убывания вероятностей. Два последних символа объединяются в один вспомогательный, которому приписывается суммарная вероятность.

Шаг 2. Вероятности символов, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последних объединяются. Процесс продолжается до тех пор, пока не получим единственный вспомогательный символ с вероятностью, равной единице.