Лекция 2.
Электродинамические основы теории антенн. Поле антенны в режиме передачи. Дальняя зона. Элементарные излучатели.
2.1 Электродинамические основы теории антенн
Достаточно общей моделью антенны в режиме
передачи является область пространства с заданным распределением тока: ![]() (рис.1).
(рис.1).
При описании антенны удобно одновременно использовать две системы координат: декартову (x, y, z) и сферическую (r, q, j), которые выбраны так, как указано на рис.1 (x=r sinq cosj, y=r sinq cosj, z=r cosq).
Из курса электродинамики [] известно, что поле заданной системы токов удобно выразить через вектор-потенциал
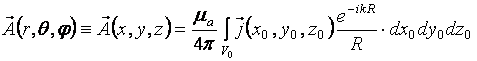 , (2.1)
, (2.1)
где
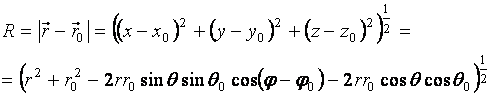
В формуле (2.1) индексом “0” помечены координаты источников поля, координаты без индекса соответствуют точке наблюдения.
Напряженности электрического и магнитного поля вычисляются по известным формулам:
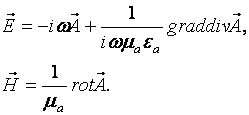 (2.2)
(2.2)
Начало координат обычно выбирается в области расположения излучающих токов, которая не выходит за сферу радиуса r0max (наибольшее удаление точек антенны от начала координат).
 |
Составляющие вектора потенциала и, соответственно, векторов напряженности поля, разлагаются по базису, связанному с точкой наблюдения (местный локальный базис). Орты этого базиса представляют единичные векторы касательные к координатным линиям, проведенным через точку наблюдения (рис.2).
Для дальнейшего полезно заметить, что декартовы составляющие вектора потенциала соответствуют декартовым составляющим плотностей тока:
 .
.
В сферических координатах это не так, поскольку орты с одинаковыми индексами в разных локальных базисах повернуты по отношению друг к другу (рис.2а).
Соотношения между ортами декартового и сферического базисов в точке наблюдения с координатами x=r sinq cosj, y=r sinq sinj, z=r cosq дается формулами:
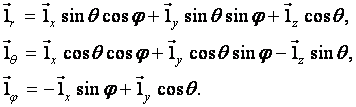 (2.3)
(2.3)
Так же как и орты декартовой системы координат, разные орты сферической системы координат попарно ортогональны, но лишь при условии, что они взяты в одной и той же точке.
Такие системы координат называются ортогональными. В этих системах координат составляющие вектора представляют его ортогональные проекции на направления ортов, а аналитически определяются как скалярные произведения вектора на эти орты.
Например:
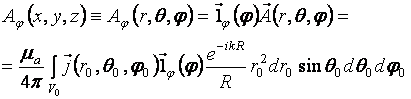 .
.
Учитывая, что
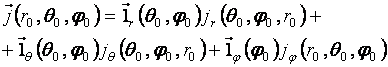 ,
,
а также формулы (2.3), получим:
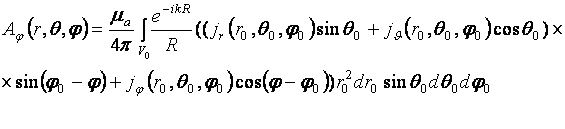 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.