Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 4: "Спутниковый транспондер (бортовой ретранслятор)" (Выходные сигналы транспондера. Высокочастотная фильтрация несущей, модулированной цифровым сигналом)

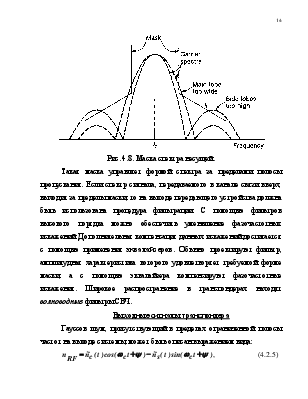
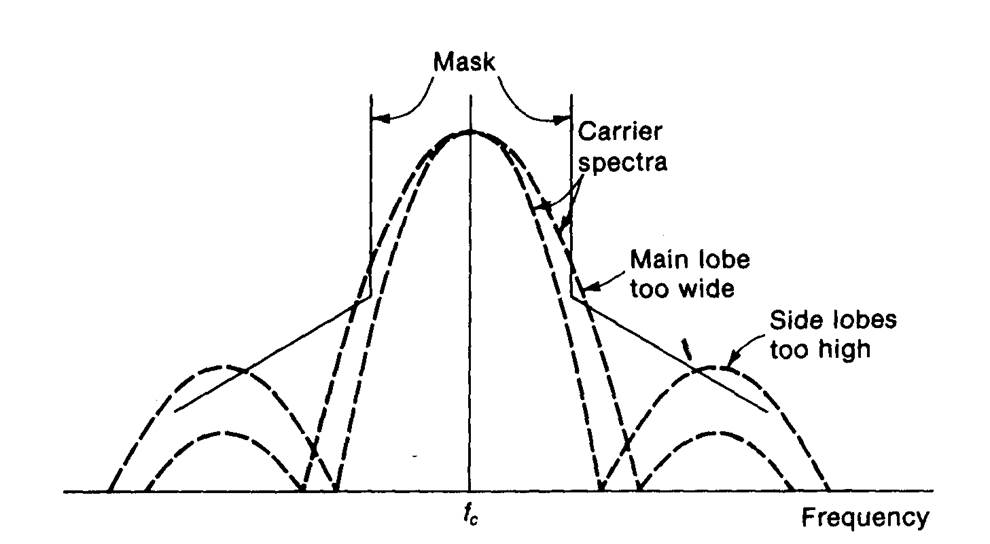
Рис. 4.8. Маска спектра несущей.

Такая маска управляет формой спектра за пределами полосы пропускания. Если спектр сигнала, передаваемого в канале связи вверх, выходит за пределы маски, то на выходе передающего устройства должна быть использована процедура фильтрации. С помощью фильтров высокого порядка можно обеспечить уменьшение фазочастотных искажений. Дополнительная компенсация данных искажений достигается с помощью применения эквалайзеров. Обычно проектируют фильтр, амплитудная характеристика которого удовлетворяет требуемой форме маски, а с помощью эквалайзера компенсируют фазочастотные искажения. Широкое распространение в транспондерах находят волноводные фильтры СВЧ.

Выходные сигналы транспондера

Гауссов шум, присутствующий в пределах ограниченной полосы частот на выходе системы, может быть описан выражением вида:

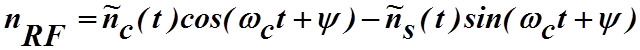,                           (4.2.5)

где y произвольный (случайный) фазовый угол;  и  – случайные квадратурные шумовые компоненты. Эти квадратурные компоненты являются низкочастотными шумовыми процессами со спектром мощности, который получен сдвигом одностороннего спектра ограниченной ширины в начало координат, как показано на рис. 4.9.

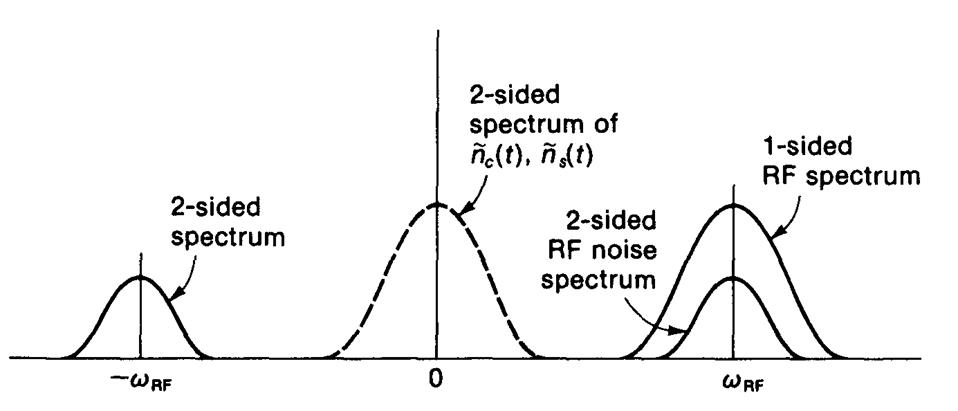
Рис. 4.9. Спектральные модели шума на выходе (–– высокочастотный шум в ограниченной полосе частот;  ---- низкочастотная шумовая составляющая спектра).

Отметим, что односторонний спектр шума становится двухсторонним шумовым спектром. В то время как спектр полосового высокочастотного шума симметричен относительно центральной частоты , шумовые компоненты  и  являются статистически независимыми процессами, кросс-корреляционная функция которых равна нулю. Если  – шумовой Гауссов процесс, и каждый процесс  и  также является шумовым Гауссовым процессом, то формула (4.5) описывает точную статистическую модель высокочастотного шума.

Влияние аддитивного полосового шума на форму колебания несущей на выходе сводится к искажению формы сигнала. Запишем несущее колебание в виде

.                             (4.2.6)

При добавлении шума к несущей получаем

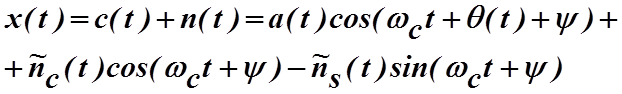.                          (4.2.7)

После тригонометрических преобразований имеем

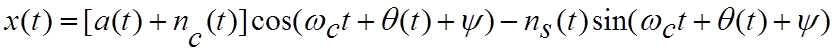,        (4.2.8)

где

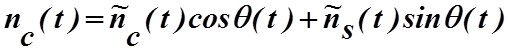
                                                                                         (4.2.9)

.

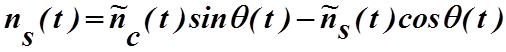Шумовые компоненты 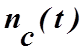 и 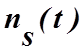 сформированы из комбинаций квадратурных компонент  и . Процессы  и   являются Гауссовыми процессами для любых функций  и эти процессы имеют одинаковые спектры при условии, что полоса частот превышает полосу частот модулирующего колебания . Уравнение (4.2.8) может переписано в виде:

,                  (4.2.10)

где

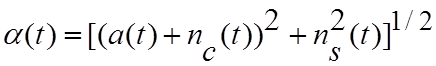,                         (4.2.11а)

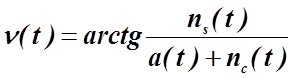.                         (4.2.11б)

В последней формуле величина n(t) определяет фазовой шум. Следовательно, эффект добавления полосового высокочастотного шума в несущее колебание в линии вверх проявляется в преобразовании амплитудной модуляции в величину a(t) в формуле (4.2.11а) и возникновении фазового шума n(t) в (4.2.11б) в фазе колебаний несущей.

Поэтому несущие колебания в спутниковых системах связи обычно имеют постоянную огибающую (a(t)=A) и поскольку уровень несущей в линии вверх превышает уровень шума, формулу (4.2.11) часто аппроксимируют выражением вида:

,                                    (4.2.12а)

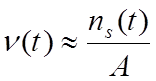.                                          (4.2.12б)

Следовательно, амплитуда искажена главным образом компонентой шума n_c(t), которую часто относят к амплитудному шуму или к синфазному шуму. Фаза искажена главным образом компонентой шума n_s(t), которую часто относят к квадратурному шуму.

4.3. Высокочастотная фильтрация несущей, модулированной цифровым сигналом

Процедура фильтрации несущего колебания, модулированного цифровым сигналом, может применяться как в пункте передачи Земной станции, так и на борту спутника – в транспондере.

Рассмотрим сигнал, поступающий на вход высокочастотного фильтра в виде колебания с постоянной огибающей и квадратурными компонентами вида

,                          (4.3.1)

где А – амплитуда несущей; m_c(t) иm_s(t) – квадратурные компоненты, модулированные данными. Спектр несущего колебания (4.3.1), равный

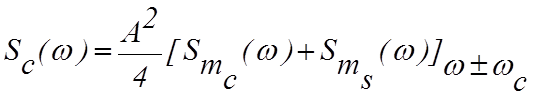,                          (4.3.2)

зависит от индивидуальных спектральных плотностей квадратурных модулирующих компонент. В результате высокочастотной фильтрации на выходе фильтра с передаточной характеристикой H_RF(w) получают спектр вида

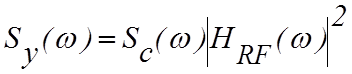.                                   (4.3.3)

Выражение для несущей на выходе фильтра представим в виде

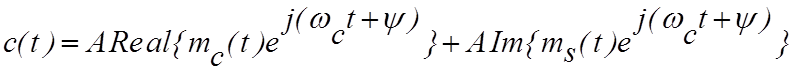,        (4.3.4)

где Re[.] и Im[.] – вещественная и мнимая часть комплексной величины, соответственно. Тогда сигнал на выходе фильтра равен

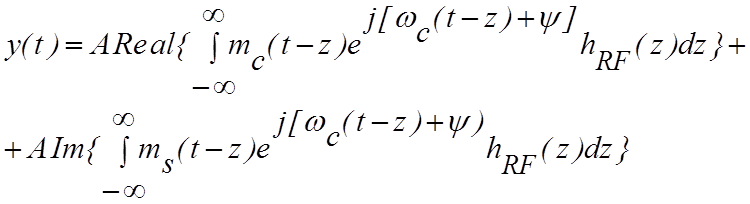,                 (4.3.5)

где h_RF(t) – импульсная характеристика полосового фильтра. Формула (4.3.5) может быть преобразована к виду

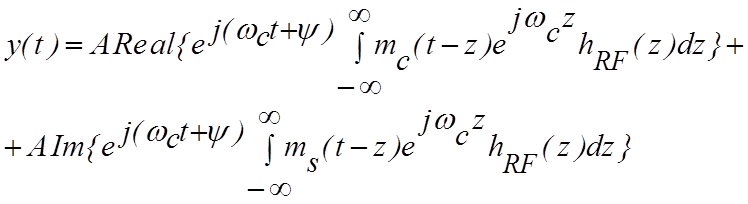.                 (4.3.6)

Интегралы в последнем выражении представлены комплексными величинами и соответствуют фильтрации каждой компоненты m(t) фильтром с импульсным откликом, равным 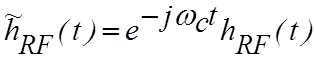. Применив преобразование Фурье к функции 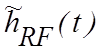, получим передаточную характеристику вида

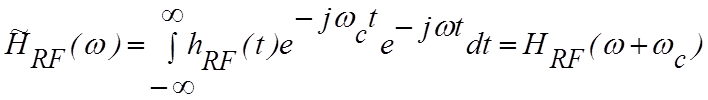.                 (4.3.7)

Последнее выражение описывает передаточную характеристику фильтра нижних частот, полученную сдвигом характеристики полосового высокочастотного фильтра от частоты w_с до частоты w= 0. Поэтому выражение (4.3.6) можно представить в виде

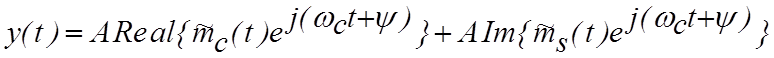,        (4.3.8)

где  и  – это функции, полученные после процедуры фильтрации функций  и . Преобразование Фурье функций  и  запишем как

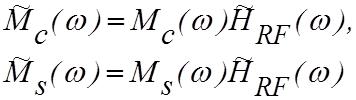.                                   (4.3.9)

Тогда спектр несущей после фильтрации равен

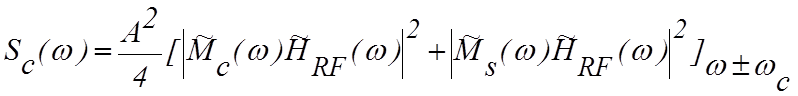.(4.3.10)

Анализ уравнения (4.3.10) показывает, что спектр (4.3.3) несущей после фильтрации соответствует высокочастотной фильтрации с частотным сдвигом цифрового колебания. Поэтому характеристики высокочастотного спектра несущего колебания могут быть определены с помощью процедуры фильтрации нижних частот. На рис. 4.10а показаны спектры колебаний QPSK на выходе фильтра Чебышева, полученные для различных значений ширины полосы частот и для различных порядков фильтров. Из графиков видно уменьшение мощности несущего колебания, хотя наблюдается также и уменьшение основного лепестка спектра при условии узкой полосы спектра.