Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 4: "Спутниковый транспондер (бортовой ретранслятор)" (Выходные сигналы транспондера. Высокочастотная фильтрация несущей, модулированной цифровым сигналом), страница 2

 

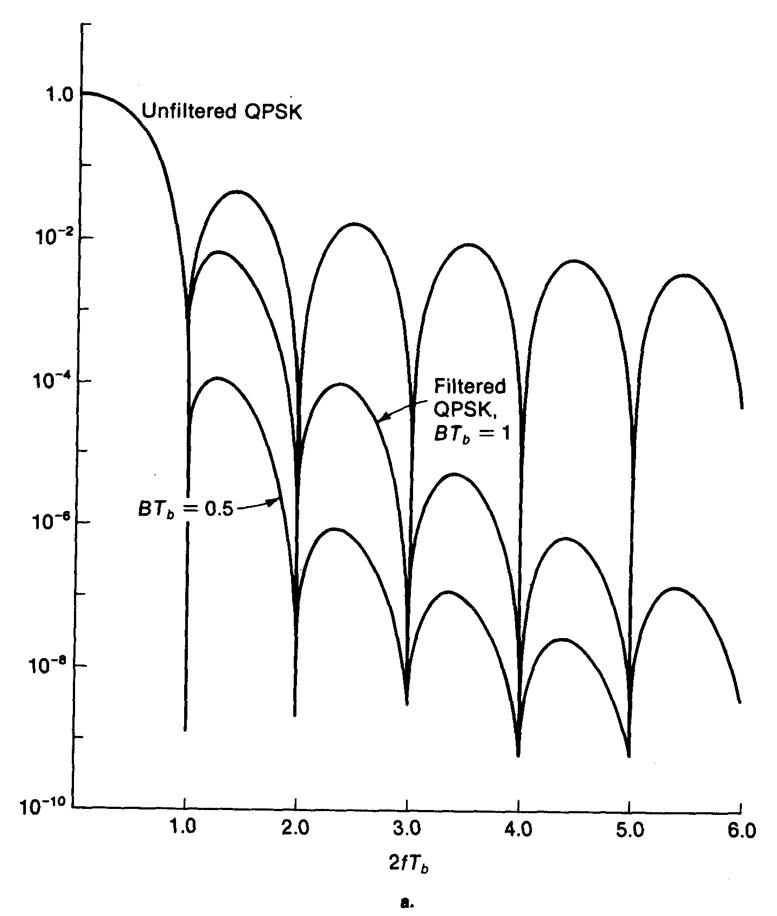
Рис. 4.10а. Спектр несущей в системе QPSK на выходе полосового фильтра Баттерворта.

Чрезмерная фильтрация при попытке уменьшения спектральных хвостов и уровня шума, однако, может породить искажения квадратурных данных. Пусть m(t) перед фильтрацией задана в виде функции NRZ как

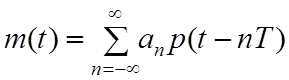,                           (4.3.11)

где p(t)=1, 0 £ t £T, a_n=±1, и T длительность бита для BPSK и длительность символа для QPSK, соответственно. Уравнение (4.3.9) показывает, что несущая на выходе высокочастотного фильтра имеет форму вида

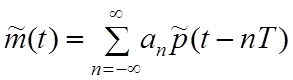,                           (4.3.12)

где  – это импульс на выходе фильтра, причем преобразование Фурье данного импульса равно

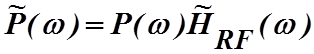,                               (4.3.13)

где P(w) – преобразование Фурье бита. Отмеченное искажение формы сигнала появляется, когда , где  – ширина полосы фильтра на уровне 3 дБ, т.е. когда ширина полосы фильтра становится меньше, чем ширина основного лепестка спектра модулированной несущей. Искажения проявляются в сглаживании прямоугольной формы импульса p(t) и в появлении "хвостов". В качестве примера на рис. 4.10б показан отклик фильтра Чебышева на единичный импульс (соответствующий цифровому сигналу) для различных порядков фильтра и для различных величин . Фильтр с чрезмерно узкой полосой приводит к уменьшению энергии импульса в течение длительности бита, а хвосты создают межсимвольную помеху в виде перетекания энергии одного бита в энергию соседнего бита. Это означает, что величина в произвольный момент времени t больше не зависит только от а_n, а эта величина подвержена межсимвольному влиянию других импульсов последрвательности данных {а_n} вследствие перекрытия импульсов .

 

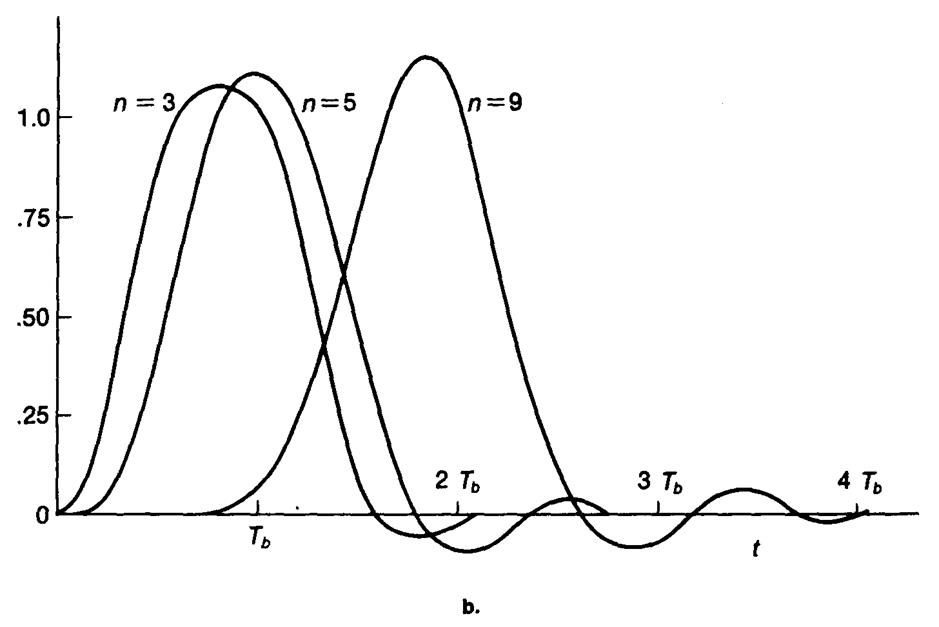Рис. 4.10б. Временной импульсный отклик на выходе фильтра Чебышева (n – порядок фильтра, BT_b = 0,5).

Искажения формы импульса приводит к ухудшению вероятности ошибки декодирования бита. На рис. 4.11а показаны результаты искажения зависимости вероятности ошибки, вызванные уменьшением величины B_RFT.

На рис. 4.11б представлены зависимости искажений, иллюстрирующие необходимость увеличения мощности несущего колебания для предотвращения потерь энергии битов и уменьшения межсимвольных искажений для поддержания вероятности ошибки передачи битов на заданном фиксированном уровне РЕ=10^-6.

 

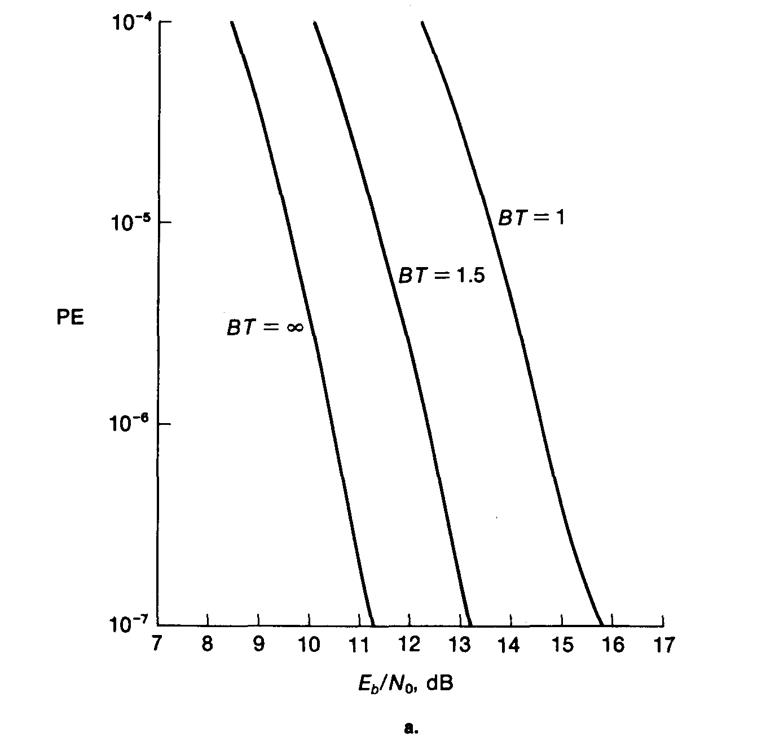Рис. 4.11а. Графики изменения вероятности ошибок в случае полосовой фильтрации колебания с модуляцией BPSK, В – ширина полосы частот на уровне 3дБ.

Таким образом, роль высокочастотной полосовой фильтрации заключается в подавлении уровня шума и уменьшении спектральных хвостов, однако фильтрация с чрезмерно узкой полосой частот требует увеличения мощности несущего колебания для поддержания требуемых показателей системы спутниковой связи. Поэтому специалисты в области телекоммуникации должны внимательно оценивать компромисс между шириной полосы частот на выходе спутниковой системы связи  и ухудшением показателей декодирования.

 

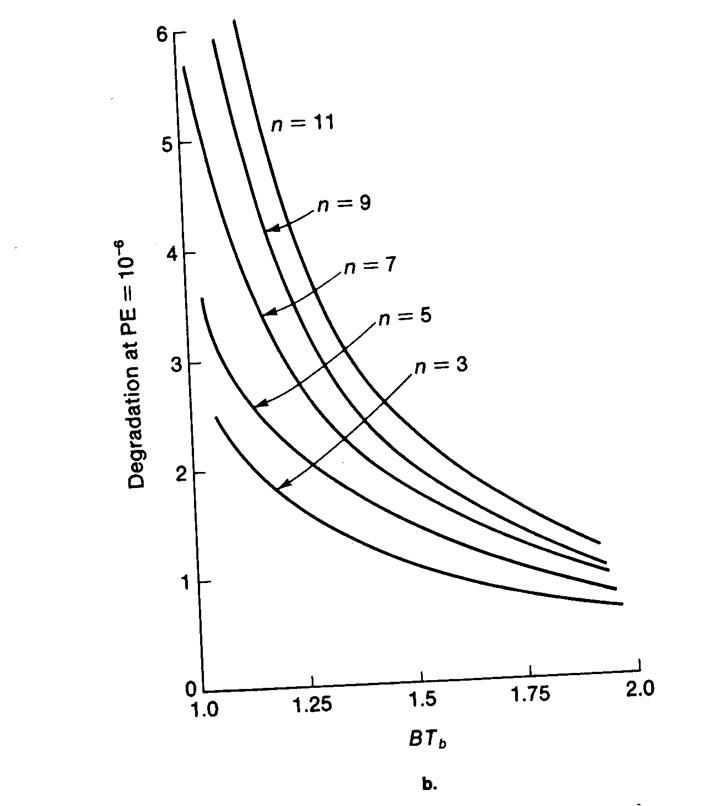
Рис. 4.11б. Требуемое увеличение энергии бита Е_b для поддержания вероятности ошибки на уровне РЕ=10^-6. Пример полосовой фильтрации колебания с модуляцией BPSK, В – ширина полосы частот на уровне 3дБ, фильтр Чебышева, n– порядок фильтра.

Другой важный эффект узкополосной фильтрации сопряжен с возможным изменением огибающей несущего колебания при поступлении на вход фильтра несущего колебания с постоянной огибающей. В произвольный момент времени t огибающая несущего колебания c(t), равная 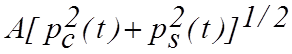, остается постоянной в любой момент времени t. Однако, колебание  в формуле (4.3.8) имеет огибающую, равную

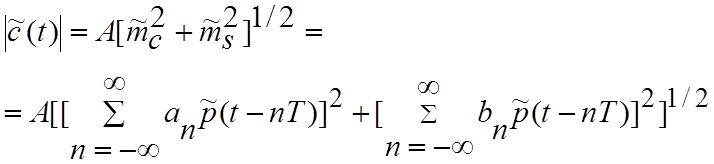.        (4.3.14)

В данном случае огибающая уже не является постоянной величиной вследствие искажений в  и вследствие эффекта межсимвольных искажений. Поэтому, высокочастотная фильтрация с чрезмерно узкой полосой частот может приводить к существенным искажениям в устройствах обработки сигналов с постоянной огибающей.

Более сложной для анализа представляется высокочастотная фильтрация фазомодулированного сигнала с постоянной огибающей. Запишем в общем виде выражение для фазомодулированного колебания как

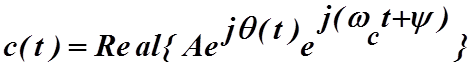,             (4.3.15)

где q(t) представляет фазовую модуляцию. Тогда сигнал на выходе фильтра в соответствии с (4.3.6) равен

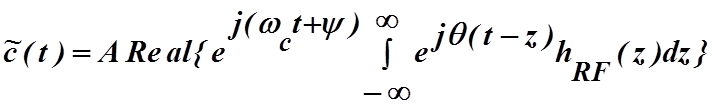     .        (4.3.16)

Последнее выражение содержит в подынтегральной функции процедуру фильтрации нижних частот комплекснозначную модулированную функцию

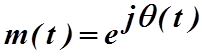                           .                                    (4.3.17)

Зная функцию , можно определить корреляционную функцию, связанную с характеристической функцией процесса q(t) и спектр мощности, связанный с суммой повторяющихся сверток спектров процесса q(t).

Если процедура свертки расширяет спектр модулированного колебания, то фильтрация позволяет уменьшить влияние свертки более высокого порядка.

Следовательно, спектр колебания (4.3.16) на выходе фильтра определяется главным образом вкладом нескольких первых членов свертки спектров q(t).

Поэтому часто пользуются аппроксимацией спектра фазомодулированного колебания на выходе фильтра вида

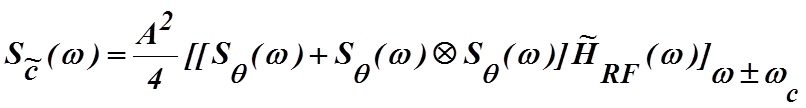,(4.3.18)

где Ä означает процедуру свертки в спектральной области.

Таким образом, согласно аппроксимации первого порядка спектр 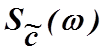 – это спектр модулированного колебания на выходе фильтра плюс результат фильтрации процесса, полученного после свертки спектра модулированного сигнала с учетом сдвига на несущую частоту.

4.4. Обработка сигналов в спутниковой системе связи

Спутниковый ретранслятор формирует несущее колебание на СВЧ для излучения в направлении Земли. Это несущее колебание может быть сформировано непосредственным частотным преобразованием (частотным сдвигом) или с помощью ремодуляции (переноса модуляции с одной несущей частоты на другую) несущей частоты.