Если вариации амплитуды несущего колебания вызваны тепловыми шумами, то соответствующие аддитивные изменения фазы проявляются в виде фазового шума. При вариациях огибающей, вызванных непосредственно модуляцией (преднамеренной или непреднамеренной), АМ/РМ преобразование в нелинейном усилителе может стать причиной модуляции информации и причиной появления перекрестной помехи.
Для аналитического исследования АМ/РМ преобразования рассмотрим несущее колебание на входе усилителя
x(t)=(A+Δ(t))cos(ωct+θ(t)), (4.6.8)
где Δ(t) представляет вариации амплитуды относительно фиксированного уровня А. АМ/РМ преобразование в усилителе может быть причиной того, что фаза несущего колебания на выходе усилителя станет равной
Ω(t)=ωct +θ(t)+Φ(Δ(t)), (4.6.9)
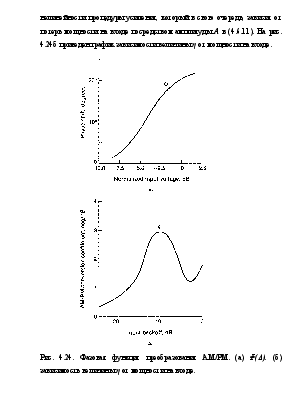
где Φ(Δ) носит название функции преобразования АМ/РМ. Типовой график функции Φ(Δ) представлен на рис. 4.24а, иллюстрирующий появление фазовых связей.
Точная математическая модель функции Φ(Δ) может быть дана в виде
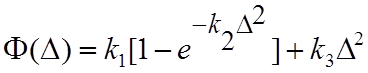, (4.6.10)
где коэффициенты k1…k3 зависят от типа ЛБВ.
Упрощенная модель, которая справедлива для малых уровней вариаций амплитуды, предполагает линейные изменения величины Φ(Δ) по отношению к вариациям амплитуды относительно выбранного уровня А в (4.6.8). В этом случае
Φ(Δ(t))=η Δ(t). (4.6.11)
Коэффициент η часто называют коэффициентом АМ/РМ преобразования усилителя. Его величина зависит от уровня нелинейности процедуры усиления, который в свою очередь, зависит от потерь мощности на входе посредством амплитуды А в (4.6.11). На рис. 4.24б приведен график зависимости величины η от мощности на входе.
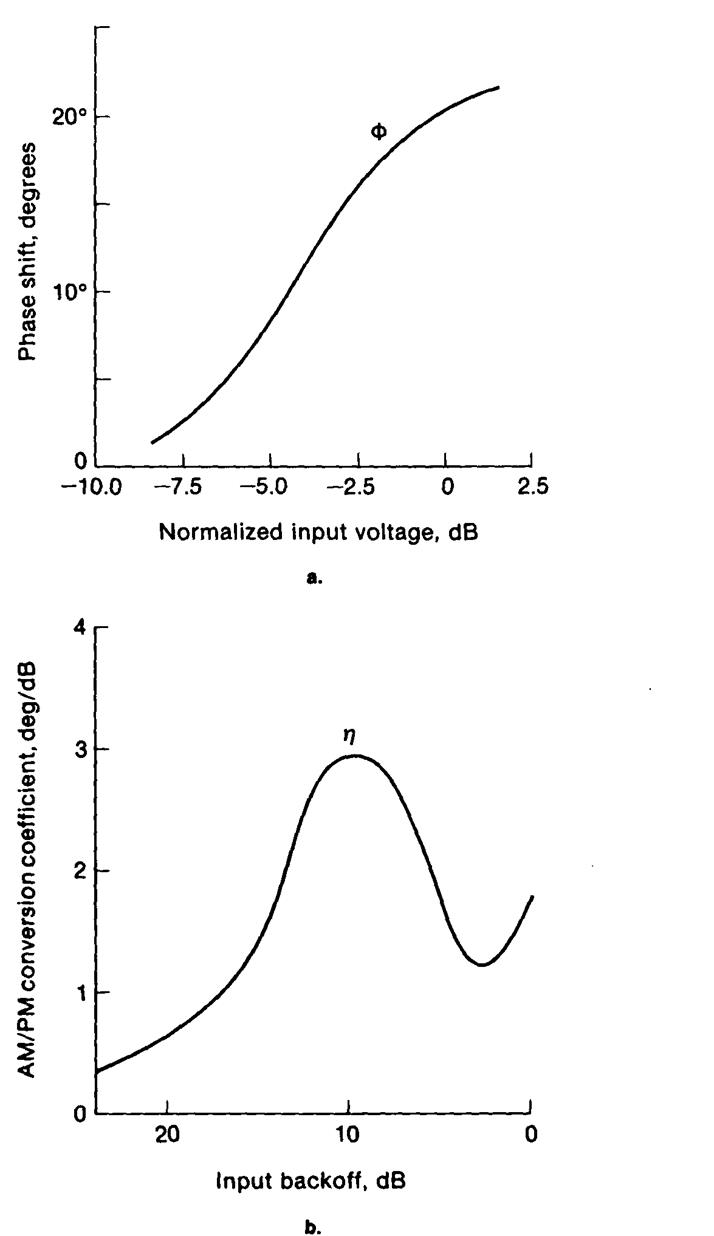
Рис. 4.24. Фазовая функция преобразования АМ/РМ. (а) Φ(Δ). (б) зависимость величины η от мощности на входе.
Когда шум приемника накладывается на несущее колебание в канале передачи вверх (см. формулу (4.2.10)) и огибающая представлена выражением (4.2.12), из (4.6.9) следует, что в канале передачи вниз в несущем колебании появляется фазовый шум из-за нелинейности усилителя. Следовательно, АМ/РМ преобразование порождает фазовый шум, мощность которого равна η2Pnu, где Pnu – это мощность шума в спутниковом канале вверх.
Комбинация преобразований АМ/АМ и АМ/РМ в ЛБВ позволяет создать обобщенную модель нелинейного усилителя мощности. Запишем колебание на входе в виде
x(t)=α(t)cos(ωRFt+θ(t)+ψ), (4.6.12)
α(t)=A+Δ(t),
тогда усиленное колебание несущей на выходе равно
y(t)=g(α(t))cos(ωRFt+θ(t)+Φ(α(t))), (4.6.13)
Φ(α(t))= Φ(α(t)-A)
где g и Φ – это функции преобразования АМ/АМ и АМ/РМ.
y(t)=Real{g(α(t)) ejΦ(α(t)) ejωRFt+jθ(t)},(4.6.14)
Следовательно, нелинейный усилитель можно представить с помощью комплекснозначного коэффициента усиления (см. рис. 4.25а). Таким образом, АМ/АМ и АМ/РМ порождают в усилителях мощности преобразование модели идеального усиления (усиление – постоянная величина) в модель с комплексным коэффициентом усиления, в которой фаза зависит от эффектов преобразования.
 |
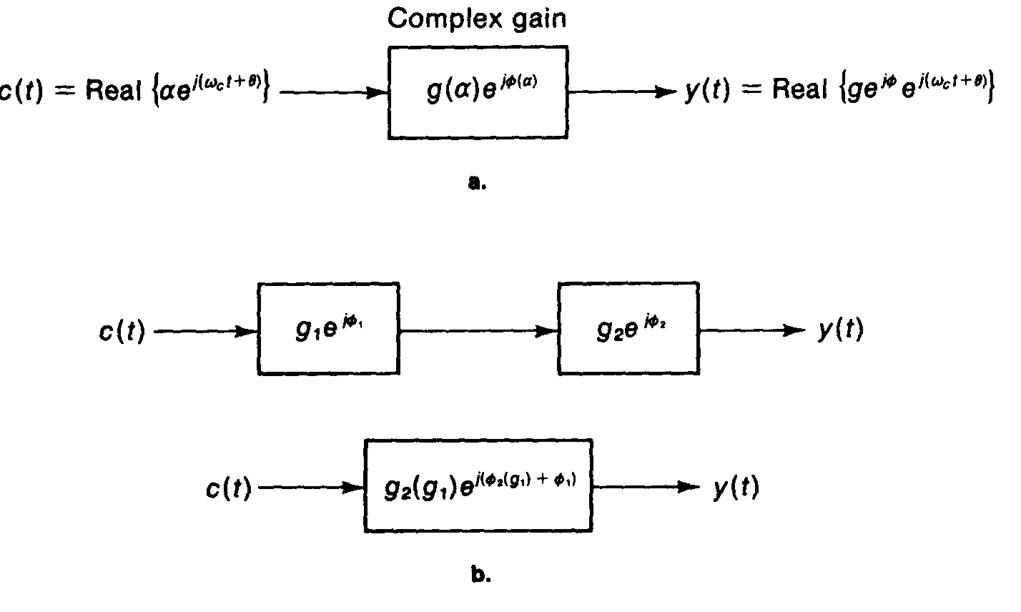Рис. 4.25. Модель нелинейного усилителя. (а) Единичная нелинейность. (б) Каскадное включение нелинейностей.
Данная модель может быть распространена на каскадное включение нелинейных усилителей (см. рис. 4.25б). Если усилители имеют функции преобразования [g1(α), Φ1(α)] и [g2(α), Φ2(α)] , соответственно, то полные функции равны
g(α)= g2 (g1(α)), (4.6.15a)
Φ(α)= Φ2(g1(α))+ Φ1(α). (4.6.15б)
Последняя модель используется при описании нелинейностей ЛБВ или усилительных устройств, которые включены до ЛБВ в виде отдельных каскадов. Отметим, что при α(t)=V (колебание несущей должно быть подвергнуто жесткому ограничению перед подачей на вход ЛБВ) выходное колебание имеет постоянную огибающую и эффект АМ/РМ не проявляется вне зависимости от влияния насыщения.
Если ограничение не используется, то усилитель или каскадное соединение усилителей можно рассматривать как мягкий ограничитель с АМ/АМ характеристикой g(α). При этом квадратурная характеристика жесткого ограничителя в (4.5.18) преобразуется к виду
, (4.6.16)
где 
и 
отфильтрованные компоненты мягкого
ограничителя, а величины 
и 
заданы в выражении (4.5.21).
4.7. Влияние нелинейности усилителя на цифровые несущие
Рассмотрим упрощенную нелинейную модель, представленную на рис. 4.26.
 |
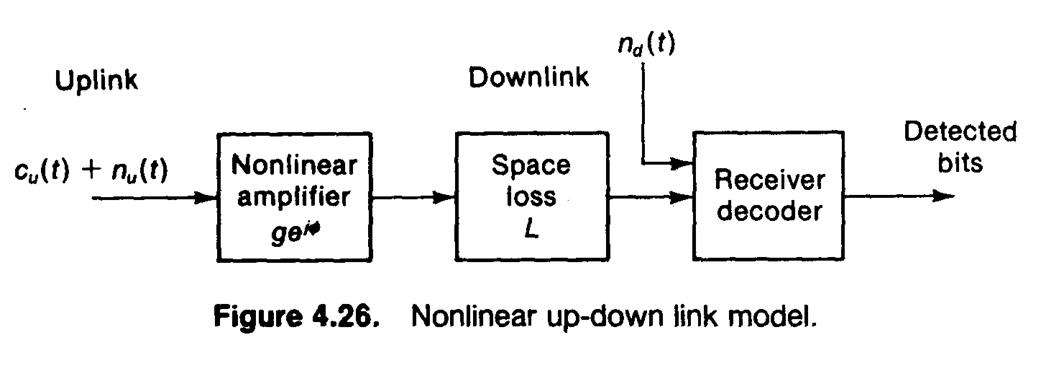Рис. 4.26. Нелинейная модель канала вверх/вниз.
Запишем выражение для несущей в канале вверх в общей квадратурной форме
. (4.7.1)
В присутствии аддитивного шума в канале вверх несущая на входе усилителя описывается выражением
, (4.7.2)
где cosθ(t)=mc(t), sinθ(t)=ms(t), и α1(t) ν1(t) – амплитудный и фазовый шум на входе усилителя. После нелинейного усиления с использованием модели на рис. 4.26 принимаемый сигнал в канале вниз имеет вид
 |
где nd(t) – шум в канале вниз. Выражение (4.7.3) с учетом квадратурных составляющих может быть преобразовано к виду
|
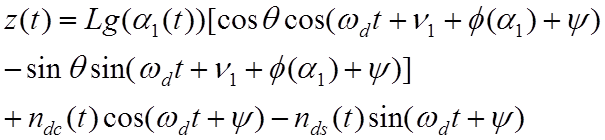
Дальнейшее преобразование дает
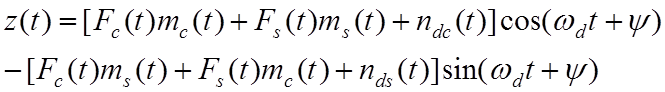, (4.7.5)
где
, (4.7.6а)
. (4.7.6б)
Таким образом, эффект нелинейного усиления при комплексной величине коэффициента усиления g(α)exp(jΦ(α)) порождает искажения и помеху в каждой квадратурной компоненте. Например, в косинусной компоненте сигнальная составляющая mс(t) умножается на искажающий член Fс(t), а квадратурная компонента ms(t) – на член Fs(t). Случайные функции Fс(t) и Fs(t) зависят от амплитудного и фазового шума в линии связи вверх, а также от преобразования АМ/АМ и АМ/РМ в ЛБВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.