Конспект лекций по курсу: «Основы построения Земных станций и бортовых ретрансляторов». Часть 4: "Спутниковый транспондер (бортовой ретранслятор)" (АМ/РМ преобразование. Влияние нелинейности усилителя на цифровые несущие), страница 2

На выходе квадратурного декодера формируются следующие компоненты

I(t) = F_с(t) m_с(t) + F_s(t) m_s(t)+ n_dc(t),                    (4.7.7а)

Q(t) = F_с(t) m_s(t) + F_s(t) m_c(t)+ n_ds(t).                   (4.7.7б)

Влияние нелинейности зависит от формата модуляции (m_с(t) и m_s(t)), типа декодирования (выборочная или согласованная фильтрация) и степени нелинейности.

Для модуляции BPSK (m_s(t) = 0, m_с(t) =±1) с длительностью бита T_b и выборочным декодированием вероятность ошибки бита равна

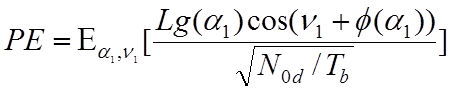,                                    (4.7.8)

где N_0d – уровень шума декодера приемного устройства, при этом выполнено усреднение случайных величин α₁(t) и ν₁(t) в течение времени наблюдения битов информации. Последние случайные величины в произвольный момент времени имеют совместную плотность распределения вероятности

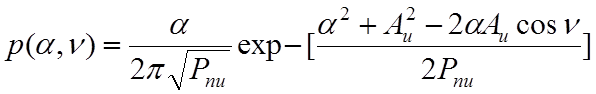,               (4.7.9)

где P_nu – мощность шума в линии связи вверх и A_u – амплитуда несущей в линии вверх. Следовательно, формулу (4.7.8) можно представить как

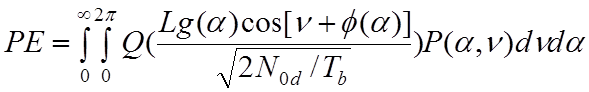.               (4.7.10)

Расчет вероятности (4.7.10) проводят численными методами. В случае жесткого ограничения  и (4.7.10) приобретает вид

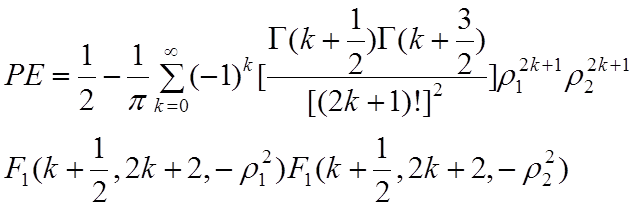,          (4.7.11)

где Γ(х) – гамма-функция, F₁ – вырожденная гипергеометрическая функция и

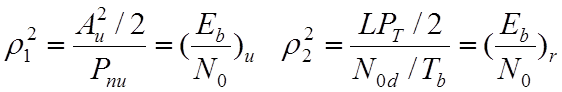.          (4.7.12)

Отметим, что ρ₁ и ρ₂ – это отношения сигнал/шум CNR в линии связи вверх (вход усилителя) и вниз (вход декодера), соответственно. Уравнение (4.7.11) отображено графически на рис. 4.27, на котором представлена зависимость вероятности ошибки (РЕ) BPSK от ρ₁ и ρ₂.

 

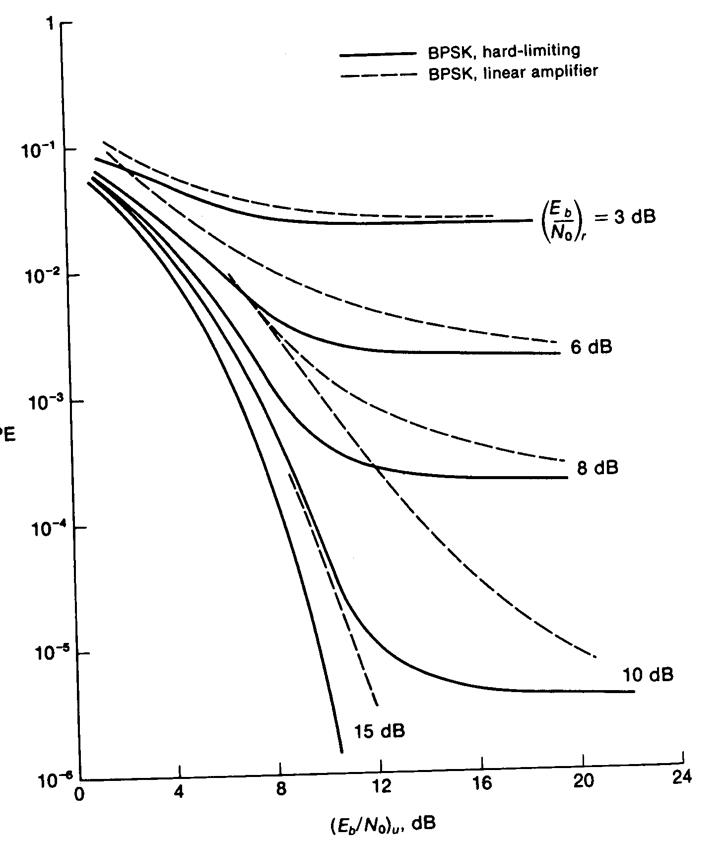Рис. 4.27. Зависимость вероятности ошибки (РЕ) в системе BPSK от E_b/N₀ в линиях связи вверх и вниз для спутникового канала с жестким ограничением.

Для квадратурной модуляции (m_s(t) ≠ 0) величину вероятности ошибки РЕ следует рассчитывать из (4.7.5), принимая во внимание помеху. Однако необходимо отметить следующее. Если при декодировании используют систему MSK и если отсчет взят в каждом канале декодирования в пиковом значении бита, то биты в квадратурных каналах пересекают нулевой уровень. Это означает, что перекрестный член равен нулю, несмотря на нелинейность, и величина РЕ такая же, как в (4.7.11). Следовательно, MSK дает результат, подобный BPSK для нелинейного канала. Для систем QPSK и OPSK квадратурный член порождает помеху, которая не может быть исключена выбором длительности бита. Поэтому следует ожидать, что QPSK и OPSK будут давать в нелинейном транспондере худший результат по сравнению с ВPSK и MSK.

В случае QPSK следует отметить, что m_s(t) будет иметь такой же или противоположный знак бита по отношению к m_с(t). Это означает, что время взятия выборки I(t) в (4.7.7) будет равно

I=F_c + F_s +n_dc                                                (4.7.13)

или

I=F_c - F_s +n_dc ,                                                                 

где F_c , F_s и n_dc – это выборочные значения функций F_c(t), F_s(t) и n_dc(t), соответственно.

Вероятность ошибки бита по каждому квадратурному каналу равна

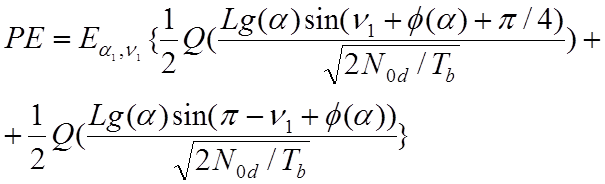.(4.7.14)

Для случая жесткого ограничения из (4.7.14) следует, что