ε
R
1 2
K (2→1) – замыкание
 |
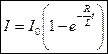Явление взаимной индукции. Взаимная индуктивность.
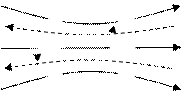
Возьмем два контура
 |
B2
B1
I1 ψ12 I2 ψ21
Взаимня индукция – явление возникновения ЭДС индукции в одном из контуров при изменении силы тока в одном из контуров при изменении силы тока в другом.
 |
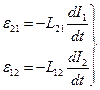ЭДС взаимной индукции.
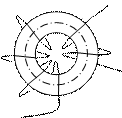
Это явление используется в трансформаторах
 |
|||
 |
|||
I1 I2
N2
N1
Ток проводимости и ток смещения. Возбуждение вихревого магнитного поля.
Имеется эл. цепь, содержащая конденсатор. Ток проводимости создает магнитное поле вокруг проводника. Согласно Максвелу переменное эл. поле между обкладками конденсатора создает также магнитное поле. В этом смысле переменное эл. поле эквивалентно некоторому эл. току, току смещения.
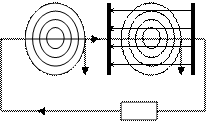Д
S
Iпр – +
Н Н
Iпр
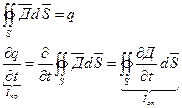Запишем
теорему Остроградского–Гауса.
 |
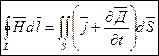– второе уравнение Максвела
Циркуляция вектора напряженности магнитного поля Н по замкнутому контуру L равна изменению электрического потока через поверхность S, охватываемую данным контуром, + токи проводимости, охватываемые данным контуром.
Полная система уравнений Максвела в интегральной форме. Их физический анализ.
 |
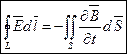– первое уравнение Максвела
Источником эл. тока являются не только электрические заряды, но и переменное магнитное поле.
|
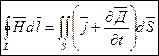– второе уравнение Максвела
Магнитные поля вызываются, либо движутся зарядами, либо переменным магнитным полем.
 |
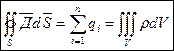– третье уравнение Максвела
Это есть обобщение теоремы Остроградского–Гауса и отражает факт, что в природе существуют эл. заряды, которые являются источника эл. поля.
 |
– четвертое уравнение Максвела
Это есть обобщение теоремы Остроградского–Гауса для магнитного поля, и отражает тот факт, что в природе отсутствуют магнитные заряды.
 |
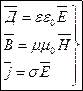– Это материальные уравнения, которые дополняют
уравнения Максвела
Система уравнений Максвела в дифференциальной форме.
К левым частям 1–го и 2–го уравнения применим теорему Стокса.
 |
– теорема Стокса
 |
|||||
 |
 |
||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.