Изучение методов регрессионного анализа, методики построения регрессионных моделей

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«БРАТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Кафедра УТС

Дисциплина: Математическая статистика

ЛАБОРАТОРНАЯ РАБОТА №4

Регрессионный анализ

Вариант 3

ОТЧЕТ

Выполнили:

студенты группы УИТС-08                                Чечулина А.А., Дианова И.Е.

Руководитель:

к.т.н., доцент                                                                               Григорьева Т.А.

Братск 2010

Цель работы: изучение методов регрессионного анализа, методики построения регрессионных моделей; выполнение расчетов простой регрессии и множественной линейной регрессии.

Задание:

1.  Расчет простой регрессии для переменных Х₁, Х₂, Х₃ по очереди, приняв переменную Х₄ за Y.

2.  Построить для каждой переменной Х_i адекватную регрессионную модель.

3.  Анализ регрессионных остатков.

4.  Сделать прогнозы для получения адекватных моделей.

5.  Расчет множественной линейной регрессии.

Исходные данные:

Вариант 3
№ п/п	Температура воздуха,ºС – х1	Отопление, Гкал/ч – х2	Вентиляция, Гкал/ч – х3	Суммарная наг- рузка, Гкал/ч – х4
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.	-12 -13 -14 -15 -16 -17 -18 -19 -20 -21	1,344 1,395 1,447 1,499 1,551 — 1,654 1,706 — 1,81	— 0,603 0,626 — 0,672 0,695 0,718 0,741 0,764 0,787	2,131 2,206 — 2,359 2,431 2,505 2,580 2,655 2,730 —

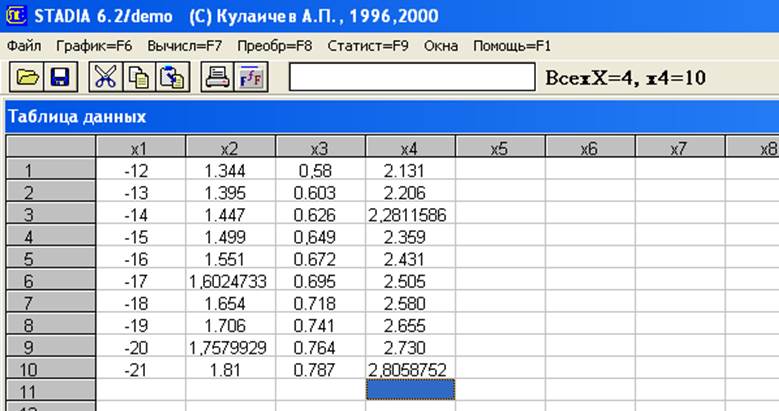
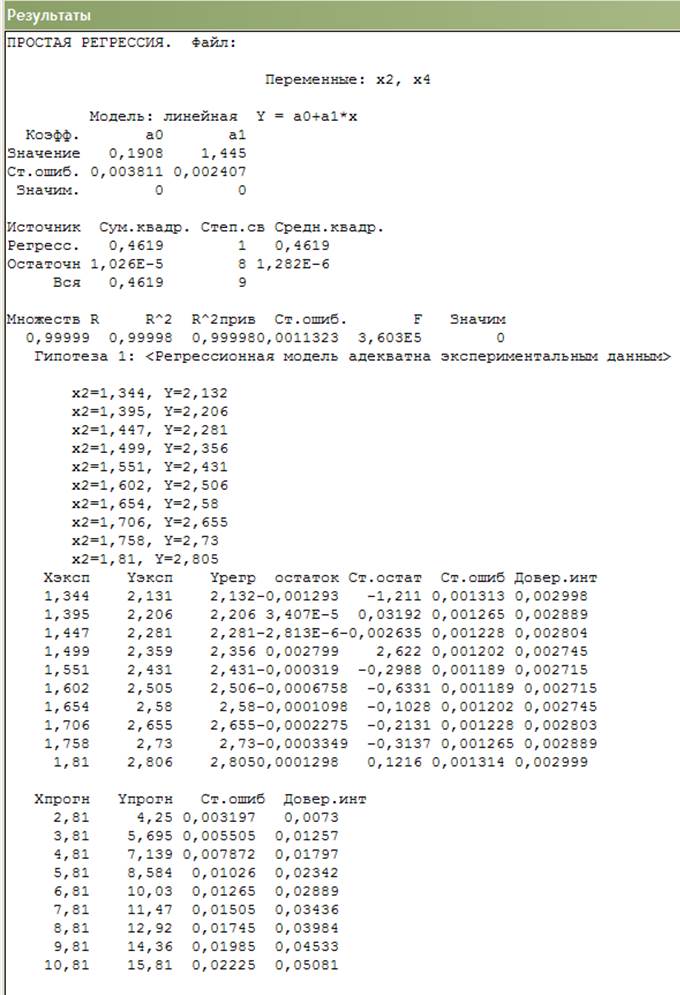
Расчет простой регрессии:

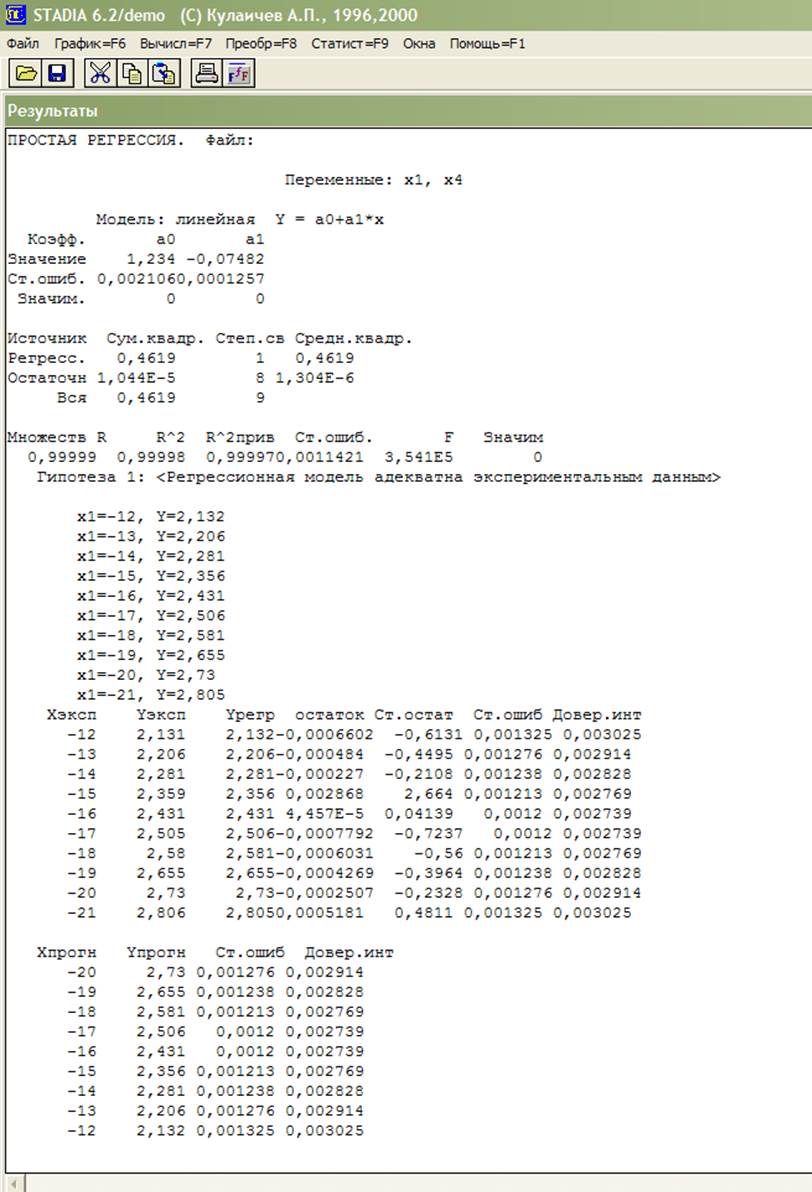
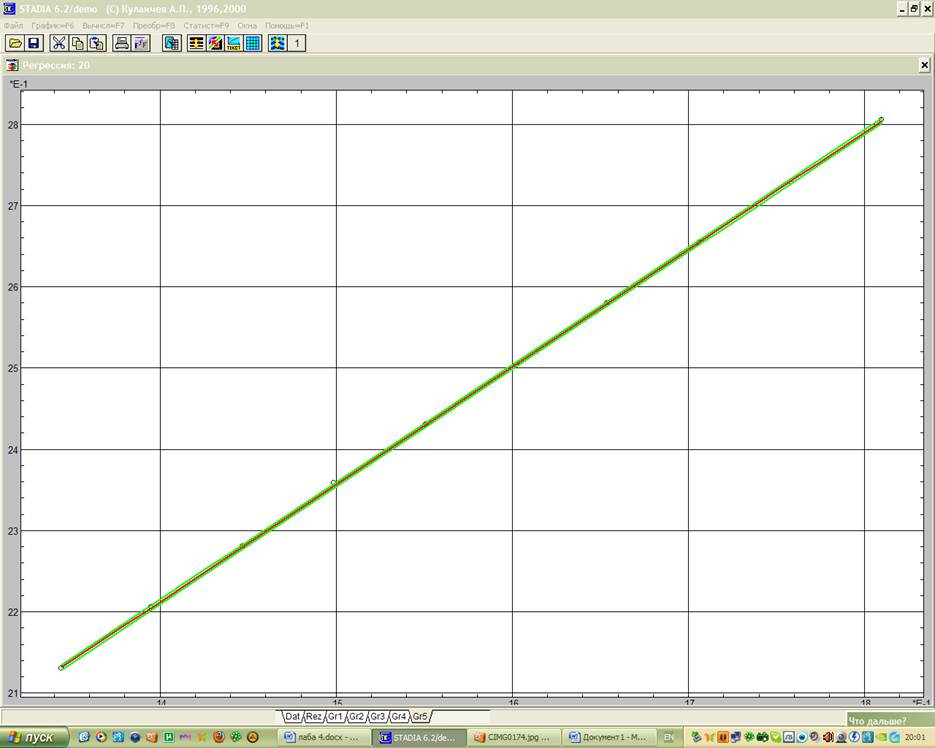
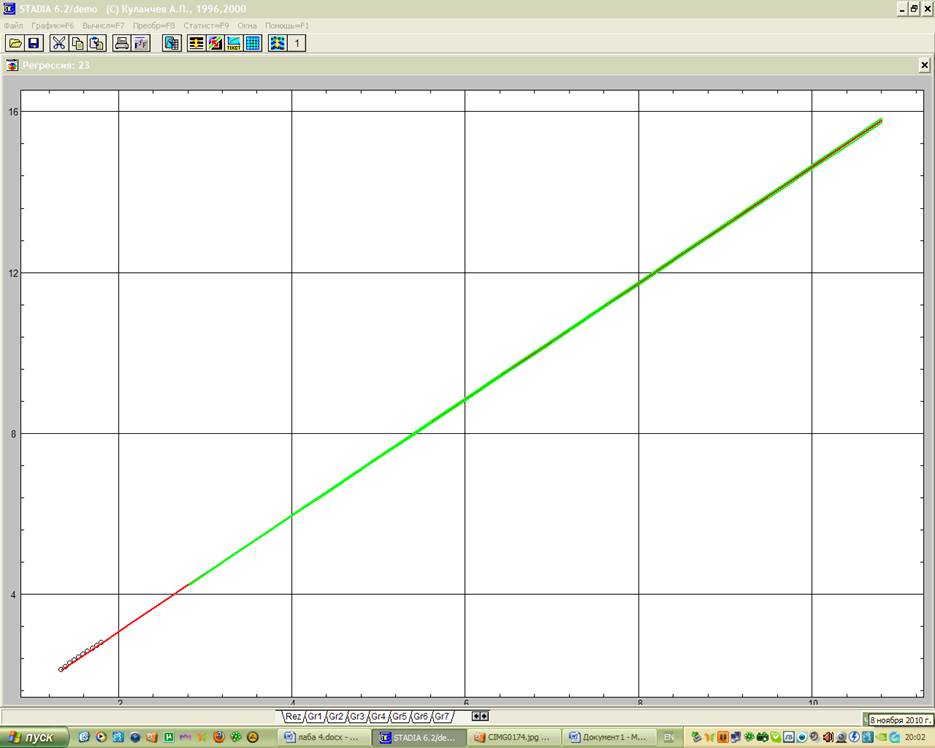
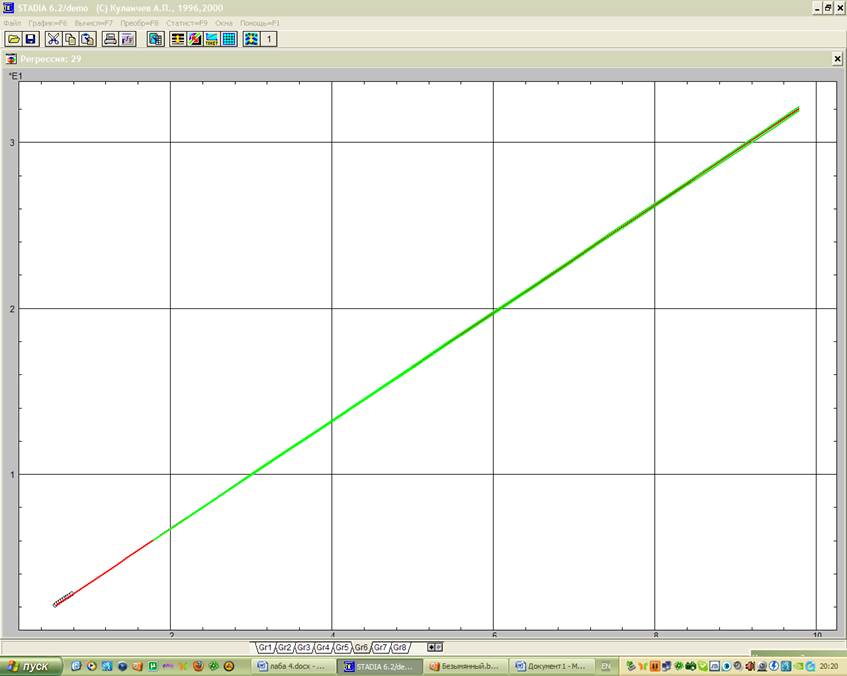
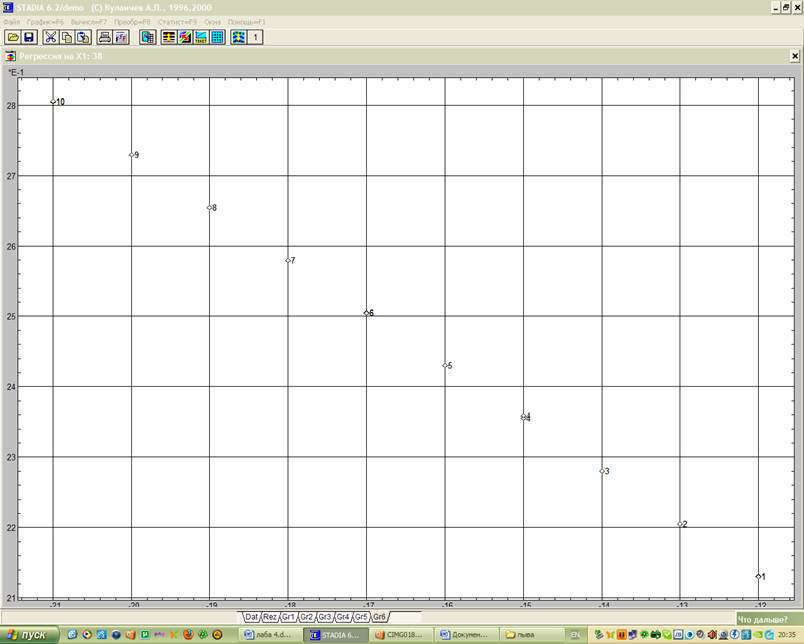
В бланке, полученном в подпункте регрессионного анализа «Простая регрессия/тренд» пункта «Статистика» выбирается соответствующая переменная Х_i и за Y принимается Х₄. Для получения представления о характере зависимости Y от Х строится функциональный график (рис. 1). После отказа от проведения процедуры интерполяции появился регрессионный график. Затем будет запрос на проведение анализа остатков, его подтвердить и осуществить прогноз.

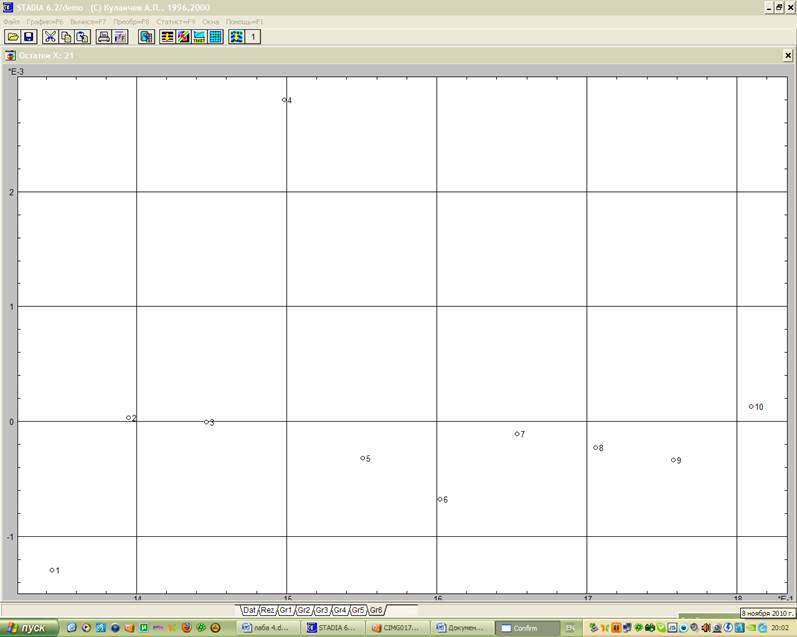
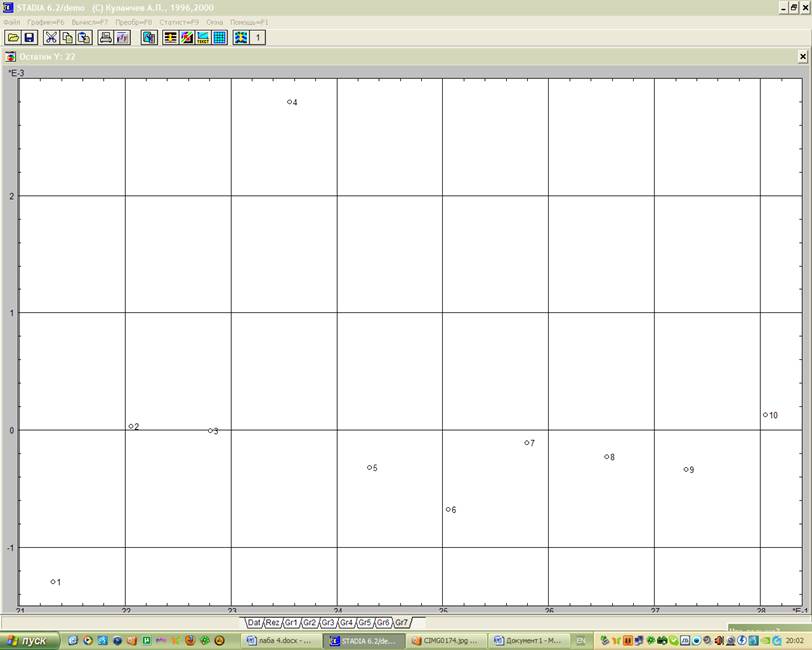
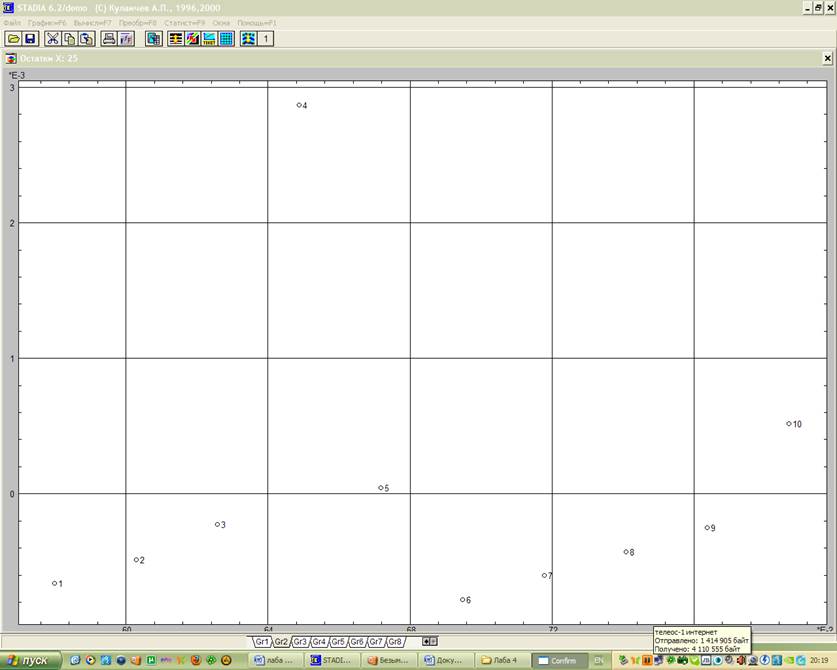
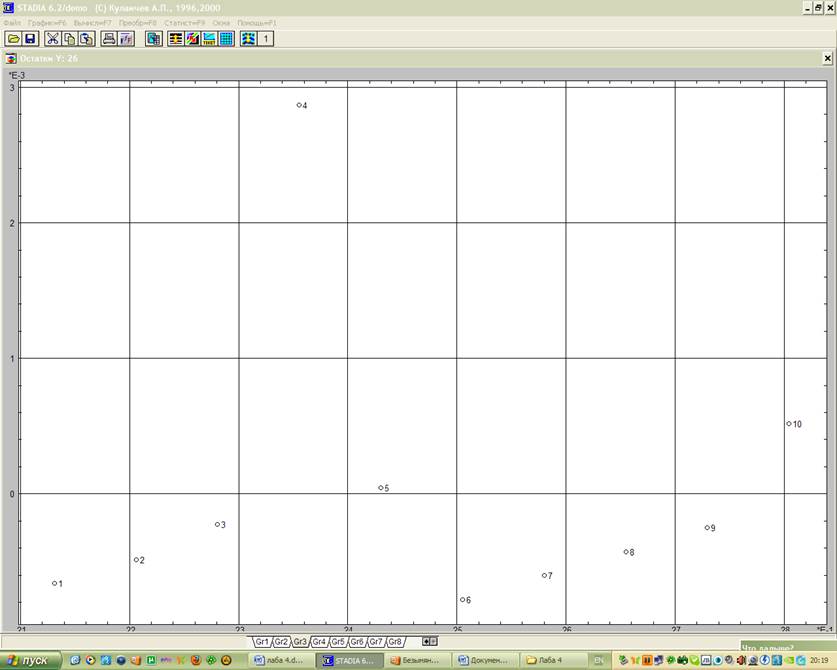
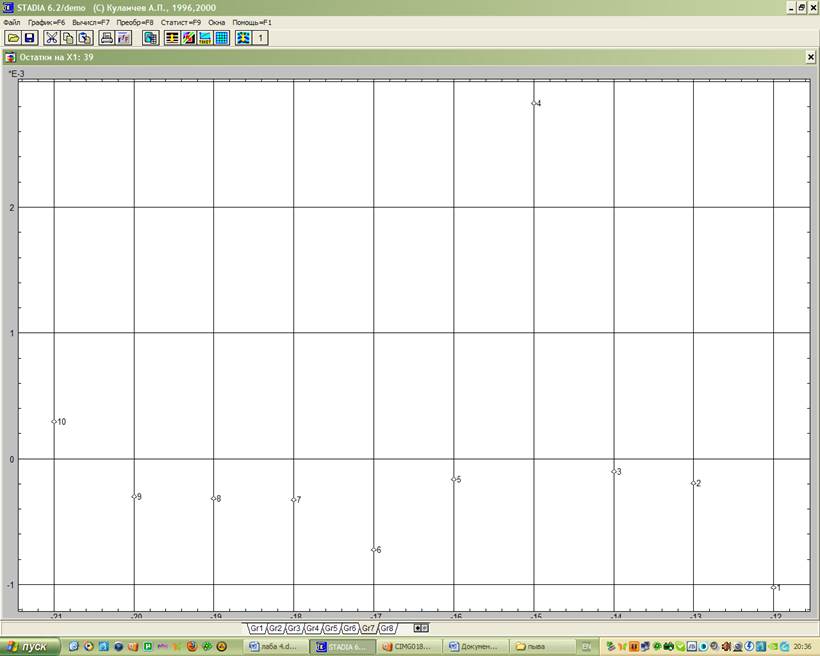
Этой цели служит также геометрический график остатков (рис. 2), сопровождающий регрессионный анализ.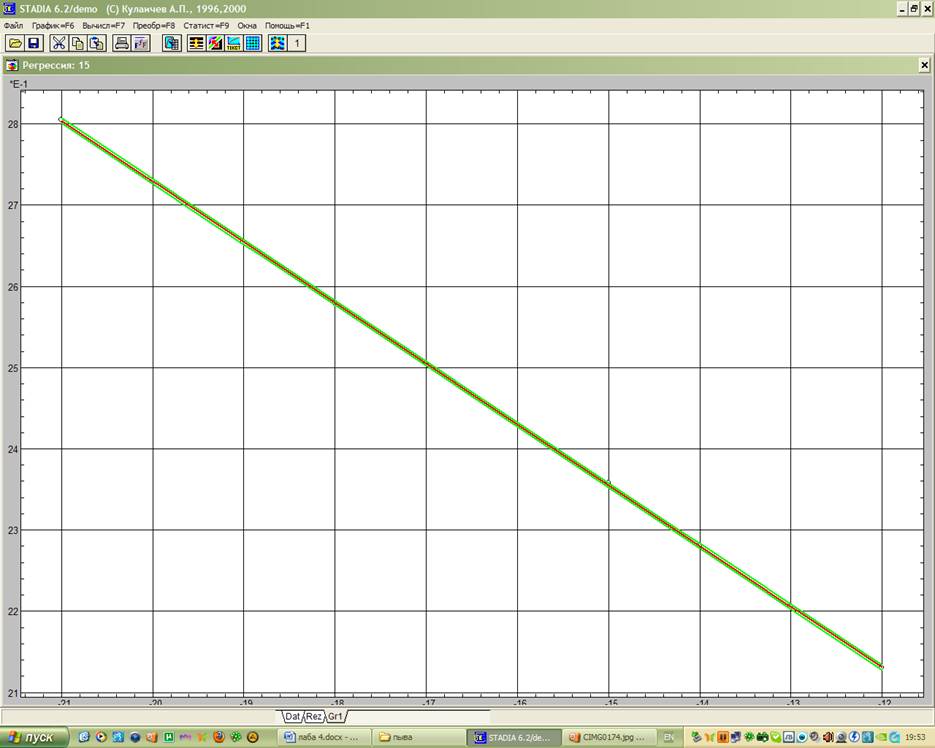

Рис.1 Функциональный график переменных Х_i и Y

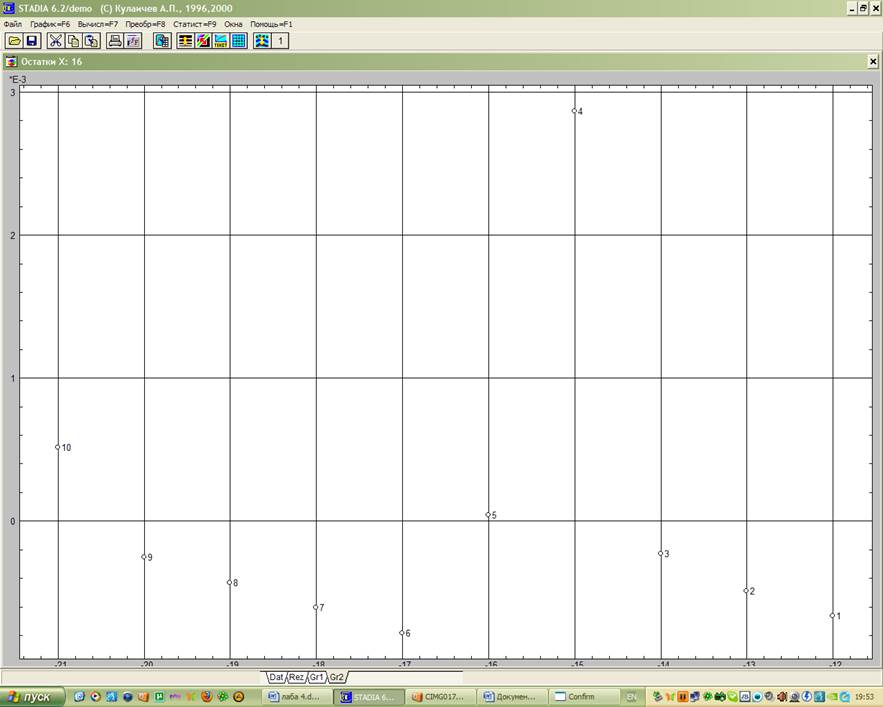
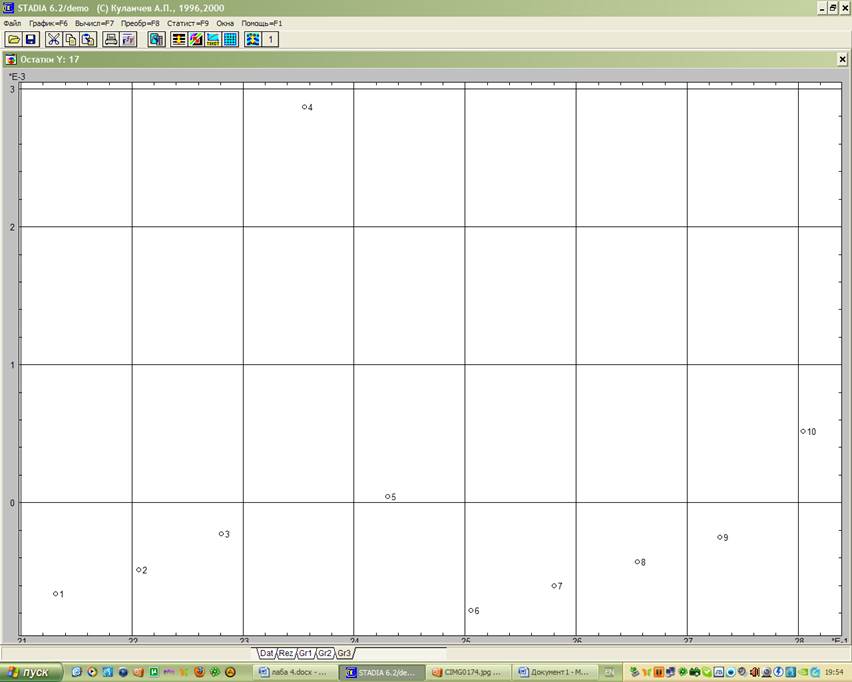
Рис. 2 Геометрический анализ остатков: а) переменной Х; б) переменной Y

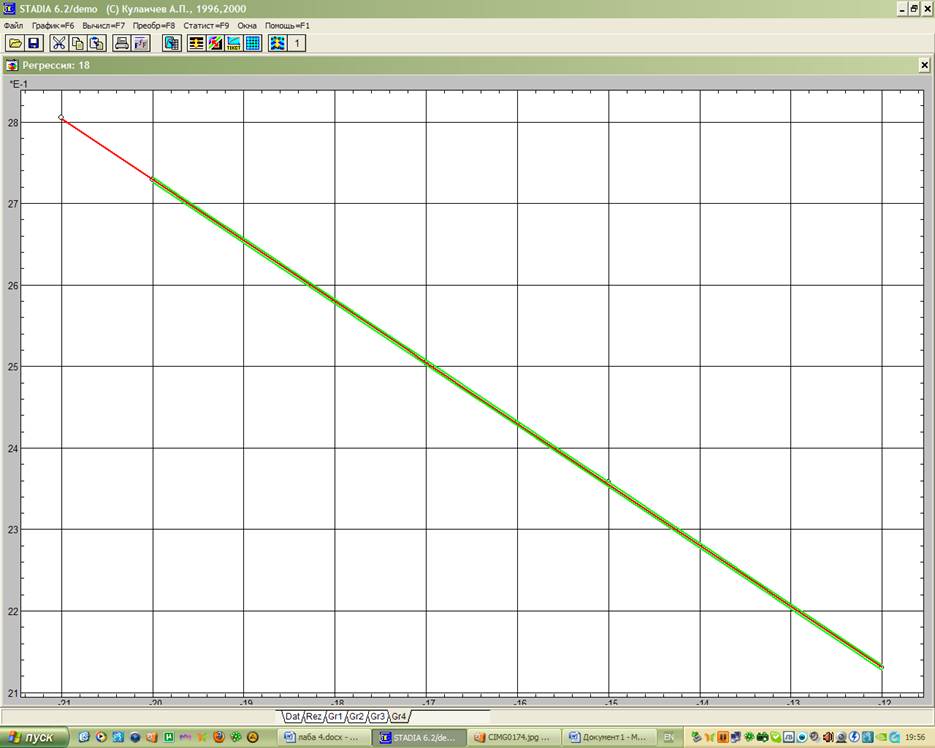
Как видно из рисунка построенная линейная модель адекватна.

Выдача прогноза производится в виде графика и в окне «Rez» появятся значения рисунка.

Выводы: как следует из числовых результатов, степенная модель адекватна экспериментальным данным – значимость нулевой гипотезы близка к нулю, на регрессионном графике (рис. 1) экспериментальные точки не выходят за доверительный интервал. Распределение остатков (рис. 2) достаточно однородно, а при их сохранении в электронной таблице и при дальнейшем анализе можно определить согласие их распределения с нормальным законом.

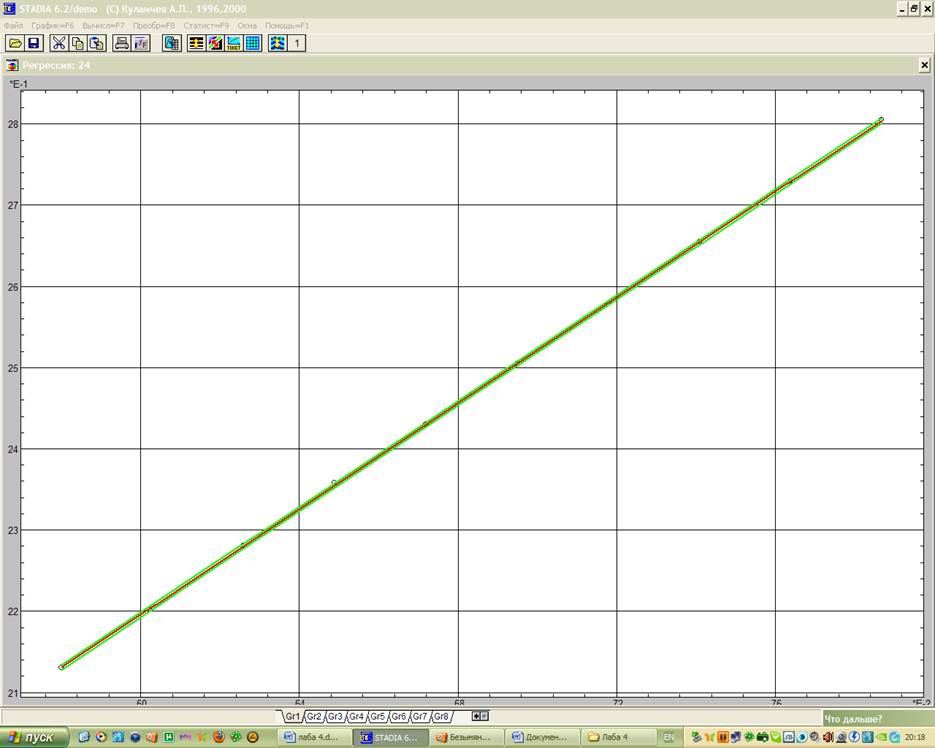
Множественная линейная регрессия

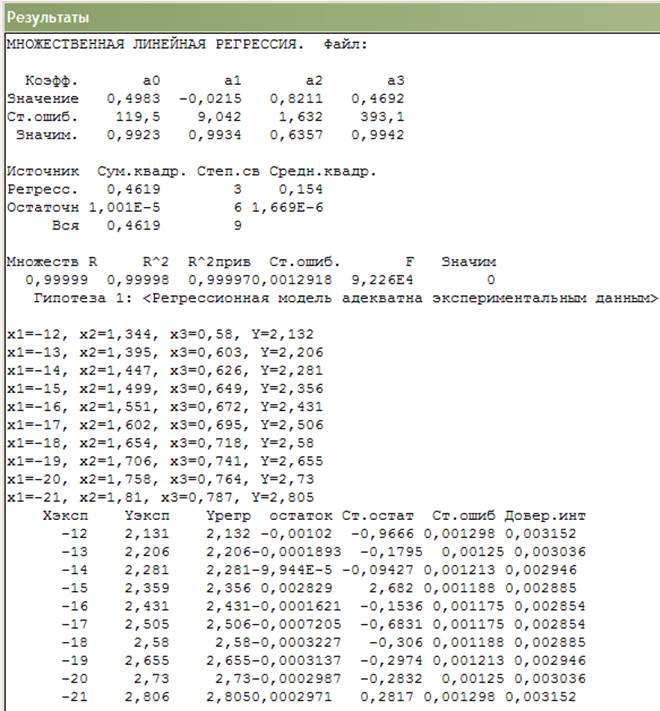
Вывод по работе: изучили методы регрессионного анализа, методики построения регрессионных моделей; выполнили расчеты простой регрессии и множественной линейной регрессии.