Электрические силы. Электрическое поле и поле магнитной индукции. Математические операции со скалярными и векторными полями. Формула Гаусса-Остроградского. Формула Стокса, страница 2

1.2. Электрическое поле и поле магнитной индукции. Соотношениями (1.1) и (1.2) введены векторные поля  и  через силу , действующую на пробный заряд  в данной точке пространства и в данный момент времени. Тем самым эти поля, как бы связывались с наличием пробного заряда. На самом деле векторы  и  являются количественной характеристикой объективно существующих полей – электрического и поля магнитной индукции, которые создаются расположенными в среде зарядами и токами (в случае вакуума заряды и токи могут быть только сторонними). Электрическое поле и поле магнитной индукции существуют и при отсутствии пробного заряда. Таким образом, с каждой точкой пространства  в момент времени  можно связать поля  и . Если поместить в эту точку пробный заряд, движущийся со скоростью , то в момент времени  на этот заряд подействовала бы сила

                                   

Нахождение распределения  функций  и по данному распределению движущихся в вакууме зарядов и токов составляет основную задачу электромагнитной теории для вакуума. В случае материальных сред ситуация существенно сложнее. Там имеются не только заряды и токи сторонних источников, но кроме них существуют еще заряды и токи самой среды. Последние зависят от полей  и , и они сами влияют на эти поля. Возникает самосогласованная, в общем случае нелинейная задача, в которой отсутствует линейная суперпозиция полей. Отражением этого факта будет то, что замкнутая система уравнений Максвелла и уравнений материальной связи (в теории сплошной среды последние – это уравнения динамики).

            Поля  и  можно изображать графически в виде силовых линий, в каждой точке которых соответствующий вектор касателен к силовой линии, а величина векторов             и  характеризует плотность распределения этих линий. Силовые линии поля  всегда начинаются на положительных и кончаются на отрицательных зарядах или на бесконечности. Если в данной точке нет электрического заряда, то через эту точку проходит только одна силовая линия поля . Силовые линии  пересекаются только в точках расположения зарядов.

1.3. Математические операции со скалярными и векторными полями. Формула Гаусса-Остроградского. Формула Стокса. Кратко напомним основные соотношения дифференциальной геометрии для векторных и скалярных функций. В декартовой системе координат  орты обозначим , тогда произвольный вектор  представляется в виде

                        ,

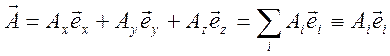где  - соответствующая компонента вектора .

            Скалярное произведение двух векторов:  

,

где  - угол между векторами.

            Векторное произведение векторов:

                                    ,

где направление орта  определяется правилом буравчика при вращении рукоятки буравчика от вектора  к вектору . Орт  ортогонален векторам  и :

                                                .

Для представления векторного произведения через компоненты векторов существует удобная форма записи в виде определителя. В декартовой системе координат имеет место представление

.

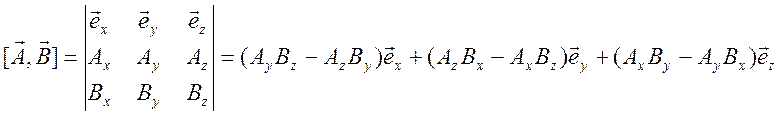В дальнейшем нам потребуются следующие соотношения:

                       

                       

            Векторная функция может быть результатом действия дифференциального оператора на скалярную функцию. Примером может служить градиент

                                    .

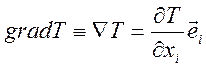Если выбрать ортогональную систему координат так, что вектор  был ортогонален поверхностям равного значения , то производные от  по касательным направлениям равны нулю. Значит, вектор  ориентирован в направлении, перпендикулярном поверхностям равного значения . Поэтому имеет место представление

                                   

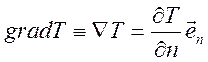
где  - координата вдоль направления .

Дивергенция (расходимость) определяется соотношением

                                                .

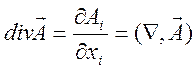Имеет место формула Гаусса-Остроградского

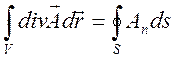                                    ,                                          (1.3)

где  - объем ограниченный замкнутой поверхностью  с внешней нормалью ,  - проекция вектора  на нормаль . 

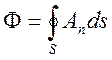 - поток вектора через поверхность .

Ротор вектора  определяется соотношением . В декартовой системе координат имеет место представление

.

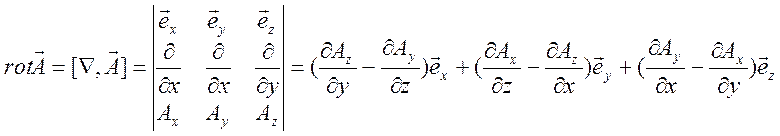Справедливы формулы

                       

где  - оператор Лапласа. В декартовой системе координат .

Для участка поверхности , ограниченного контуром  справедлива формула Стокса

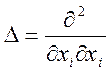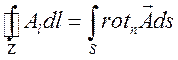                             ,                                                                (1.4)

где   - нормальная к поверхности  компонента . Направление интегрирования вдоль контура  и направление нормали связаны правилом буравчика. Интеграл по замкнутому контуру в формуле Стокса называется циркуляцией вектора  вдоль контура , а интеграл по поверхности  есть поток вектора  через поверхность .