Цифровые и логические устройства, страница 7

Последовательные устройства обладают памятью. Для них выходные переменные в какой-то момент времени зависят от входных переменных за весь предшествующий период. К последовательным устройствам относят, прежде всего, различные триггеры, а так же типичные устройства с памятью, счётчики, регистры, элементы памяти и сложные арифметико-логические узлы (процессоры).

Существуют и комбинированные, аналого-цифровые устройства. Прежде всего, это аналого-цифровой преобразователь, АЦП, и цифро-аналоговый преобразователь, ЦАП. Первый осуществляет важную операцию дискретизации  сигнала, т.е. преобразует аналоговое напряжение в последовательность чисел, таблицу. Второй  осуществляет обратную операцию и превращает последовательность чисел в аналоговое напряжение.

Рассмотрим коротко некоторые из названных устройств. Начнём с комбинационных.

8.5. Комбинационные логические устройства. Сумматоры.

Сумматоры реализуют важную операцию сложения двух двоичных чисел. Если числа многоразрядные, то это устройство сложное.

Мы рассмотрим простой пример одноразрядного сумматора. На схемах его обозначают так, как на рис. 8.17а. Имеем три переменные на входе и две выходные:  - две двоичные цифры; s – результат их сложения в выделенном разряде;  - сигналы переноса от предыдущего разряда и новый сигнал в

в следующий разряд. Таблица этой операции выглядит следующим образом.

Простой анализ таблицы позволяет нарисовать функциональную схему сумматора, рис. 8.17б.

Определим аналитический вид логических функций , составив и упростив их полную логическую единицу.

 .

.

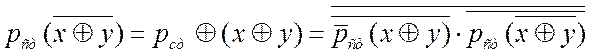Схема, реализующая операцию , была приведена раньше. На функциональных схемах она часто обозначается символами М2 (сложение по модулю 2). Можно теперь реализовать функции  совсем отдельно, как это указано на функциональной схеме. Однако разумно использовать некоторые общие части этих функций. Например, один из вариантов реализации сумматора на элементах Шеффера приведён на рис. 8.18.

В многоразрядных последовательных сумматорах сложение происходит последовательно для каждого разряда, начиная с младшего. При этом можно использовать один и тот же сумматор для всех разрядов. Однако, при таком способе суммирования, процесс занимает много времени, если число разрядов большое. Для сокращения времени поступают, например, так. Сначала производят параллельное (одновременное) суммирование двоичных цифр во всех разрядах без учёта сигналов переноса (их запоминают). А затем, в несколько этапов, суммируют сигналы переноса и формируют результат. При таком способе надо иметь много одноразрядных сумматоров, но более простых. Таким образом, уменьшение времени суммирования достигается за счёт усложнения схемы. На практике используются очень много специальных приёмов для ускорения и упрощения операций суммирования.

8.5.1. Преобразователи кодов. Шифраторы и дешифраторы.

Преобразователи кодов находят чрезвычайно широкое применение. Они имеют m входов и n выходов. Схемное обозначение приведено на рис. 8.19а.

 Шифраторы и дешифраторы являются частными случаями преобразователей кодов. Шифраторы (Coder, обозначение на схемах CD) преобразуют единичный сигнал на одном из входов в n – разрядный двоичный код. Дешифраторы (decoder, обозначение DC) преобразуют двоичный входной код в единичный сигнал на одном из выходов. Приведём примеры названных устройств.