Рассмотрим основные временные параметры разряда. По данным, приведенным в литературе одиночный стример распространяется достаточно быстро. Даже опираясь на минимально возможное значение скорости стримера [1, стр. 44] - 430∙103 м/с, мы получаем, что промежуток в 20 см стример перекрывает за 0,46 мкс. Длительность фронта стандартного грозового импульса напряжения составляет 1,3 мкс, характерная длина импульса – 53 мкс. Это значит, что за время распространения стримера напряжение не успевает существенно измениться. С другой стороны, за время импульса может возникнуть множество независимых стримеров, возникающих в различные моменты воздействия грозового импульса, имеющего ниспадающий задний фронт
Вполне возможно, что именно со спадом напряжения импульса связано различие длин отдельных стримеров на каждой фотографии в рамках воздействия отдельного импульса. На рисунке 23 приведен типовой пример – на одной фотографии видны стримеры разной длины. На графике приведена форма импульса напряжения и отмечены моменты времени, когда в соответствии с расчетом могли развиться стримеры, видимые на фотографии.
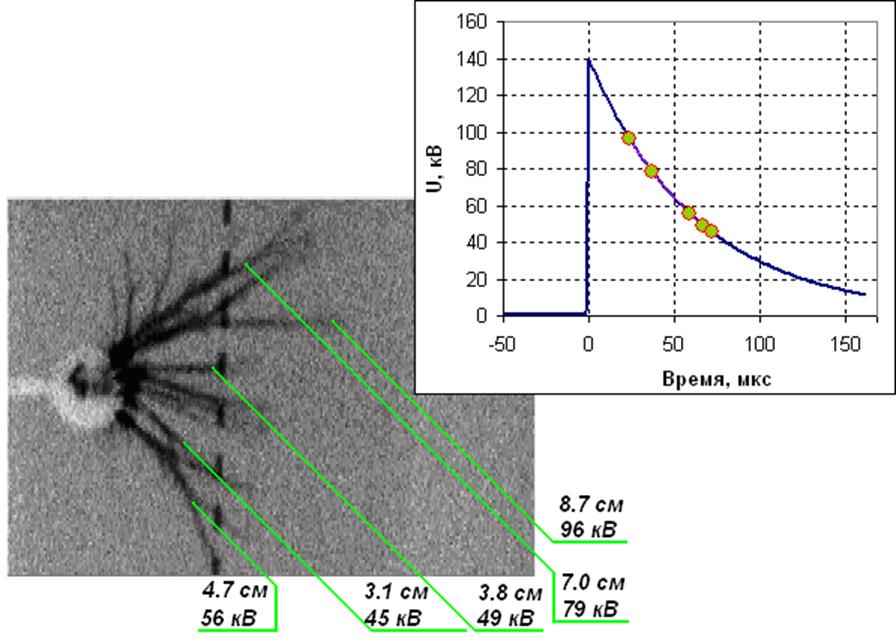
Рисунок 23. Различная длина стримеров. Расчетные напряжения, соответствующие этим длинам. Осциллограмма импульса напряжения, точки на осциллограмме - моменты, когда в соответствии с расчетом могли развиться стримеры, отмеченные на фотографии. Отрицательные стримеры, радиус сферы r=15 мм, межэлектродное расстояние h=125 мм, напряжение U=140 кВ.
Поскольку интервал импульса напряжения, в течение которого могут появиться и развиться отдельные стримеры, составляет 50 мкс и более, то за это время могут развиться сотни стримеров, не перекрываясь во времени!
Могут ли не одновременно развивающиеся стримеры влиять друг на друга? Стример распространяется быстро, но даже после затухания и остановки, остается и существует ионный след. Электронов там нет, но он является заряженным медленными ионами. Время нейтрализации и релаксации заряда ионного канала оценено в следующем пункте.
Время распространения стримеров мы оценили в предыдущем пункте – это 0,5 мкс и менее.
Время развития лавины еще меньше, чем время распространения стримеров. Лавина развивается на отрезках 1 мм и меньше, при пороговой напряженности поля E=25 кВ/см можно оценить максимальное время развития лавины:
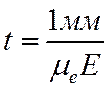
При подвижности электронов 0,06 м2/(В∙с), получаем t=7 нс, это пренебрежимо мало по сравнению с временем распространения стримера.
Оценим теперь время ожидания затравочного электрона. Каким образом инициируется разряд? И в случае положительного, и в случае отрицательного стримеров, электрон должен попасть в небольшую область у острия, где поле превышает 25 кВ/см, чтобы был возможен лавинный процесс. Иначе электрон просто прилипнет к молекуле кислорода. В случае отрицательного стримера (отрицательного острия) такой электрон может образоваться в результате попадания положительного иона на катод и вторичной эмиссии. В случае положительного острия отрицательный ион, попавший в прианодную область, где поле значительно, теряет электрон. Разные источники приводят разные критические поля, выше которых потеря электрона очень вероятна. Например, в одном из современных источников – 34 кВ/(см∙атм) [, С.124]. Таким образом, ситуация в некотором смысле симметрична – в обоих случаях разряд может быть инициирован ионом, попавшим на острие.
Какова частота падения ионов на острие? Здесь следует учесть, что силовые линии стягиваются к острию, то есть ионы, образовавшиеся из-за космического излучения, будет «собираться» на кончик иглы из широкой области. Для оценок используем поле сферического электрода. Напряженность поля дается в таком случае выражением:
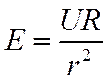
Здесь R – радиус электрода, U – напряжение. Время t, необходимое иону, чтобы пройти от радиуса r до поверхности электрода, равно:
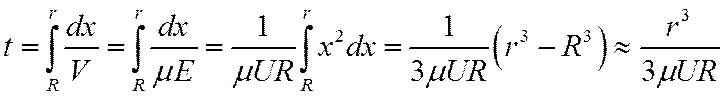 (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.