Описание лабораторной работы "Исследование кривой Пашена самостоятельного разряда в воздухе"

СПбГУ

Физический факультет

Направление

 «Прикладные математика и физика»

НОЦ «Электрофизика»

Описание лабораторной работы

Исследование кривой Пашена самостоятельного разряда в воздухе

Составили: проф. Стишков Ю.К., программист Афанасьев С.Б.

Санкт Петербург

2007

Оглавление:

1.  Цель работы

2.  Предварительные сведения

3.  Описание экспериментальной установки

4.  Принцип работы стенда

5.  Задание на предварительную подготовку

6.  Задания на проведение работы

7.  Порядок проведения экспериментов

8.  Обработка экспериментальных данных

9.  Контрольные вопросы

10. Литература

Лабораторная работа № 2

Исследование кривой Пашена самостоятельного разряда в воздухе

1. Цель работы

Получить и исследовать вольтамперные характеристики газового разряда при различных давлениях, а также получить зависимость напряжения возникновения самостоятельного разряда в воздухе от внешних параметров (кривую Пашена) для системы электродов игла-плоскость.

2. Предварительные сведения

В теории Таунсенда [1-5] прохождения электрического тока через газ учитывается ударная ионизация атомов и молекул газа электронами и положительными ионами. Для простоты электроды разрядной трубки будем считать плоскими. Рекомбинацией ионов и электронов пренебрежем, предполагая, что за время прохождения между катодом и анодом эти частицы не успевают рекомбинировать. Кроме того, ограничимся стационарным режимом, когда все величины, характеризующие разряд, не зависят от времени. Поместим начало координат на поверхности катода К, направив ось X в сторону анода А. Пусть n_e(х) и n_p(х) — концентрации электронов и положительных ионов, а υ_e и υ_p — их средние дрейфовые скорости (по абсолютной величине). Возьмем в газе бесконечно тонкий плоский слой, параллельный плоскостям анода и катода, и выделим на нем единичную площадку. Через эту площадку слева в слой ежесекундно входит n_e(х)∙υ_e(х) электронов, а справа выходит n_е(х+dx)∙υ_e(x+dx). В объеме dxслоя из-за ионизации электронами ежесекундно возникает a∙n_e∙υ_e∙dxэлектронов и столько же положительных ионов. Аналогично из-за ионизации положительными ионами образуется β∙n_p∙υ_p∙dxэлектронов и столько же положительных ионов. Наконец, может существовать внешний источник ионизации, создающий ежесекундно qпар ионов в единице объема газа. А так как в случае стационарности процесса число электронов в слое не меняется, то должно выполняться соотношение

.

Аналогично, для положительных ионов, движущихся от анода к катоду,

.

Заменяя разности соответствующими дифференциалами и сократив на dx, получим

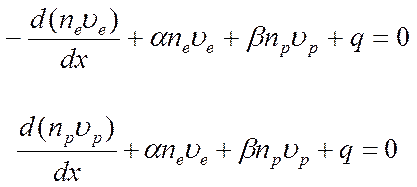
Исследуем, теперь, зависимость коэффициентов ионизации α и β от напряженности электрического поля Е и давления газа P. Для определенности будем рассматривать электроны. Примем вместе с Таунсендом, что при каждом столкновении электрон теряет скорость, которую он приобрел в электрическом поле. Чтобы электрон мог ионизовать газ, он должен на пути свободного пробега x приобрести энергию, не меньшую энергии ионизации, т.е. величина x должна удовлетворять условию x∙E ≥ V_i, где V_i - потенциал ионизации. Будем считать, что все такие электроны ионизуют газ. Возьмем пучок из N₀электронов, которые начали двигаться в электрическом поле Е с нулевой начальной скоростью. Как известно из кинетической теории газов, среднее число электронов, проходящих путь х без столкновений, будет , где  - средняя длина свободного пробега электрона. Если взять , то, согласно нашему предположению, все такие электроны будут ионизовать газ. На пути 1 см электрон испытывает в среднем  столкновении, так что на этом пути все N электронов вызовут ионизаций. Среднее число ионизации, производимое на том же пути одним электроном, будет

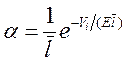
Это и есть коэффициент ионизации. Средняя длина свободного пробега  обратно пропорциональна давлению газа: , так что

где А и B — постоянные. Отсюда следует, что

т.е. отношение α/P зависит не от Е и Pв отдельности, а только от их комбинации E/P. Понятно, что этот результат (3), пока функция f не фиксирована, является более общим, чем результат (2). Таунсенд экспериментально подтвердил справедливость соотношения (3) для ряда газов. Более поздние исследования показали, что при давлениях, больших атмосферного, это соотношение удовлетворяется значительно хуже, чем для низких давлений, а при очень высоких давлениях (значительно выше атмосферного) перестает быть верным.

Простым дифференцированием по Pлегко убедиться, что при заданном значении Е выражение достигает максимума при P=Е/В. Максимальное значение α при этом оказывается равным