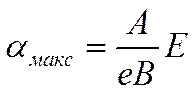Описание лабораторной работы "Исследование кривой Пашена самостоятельного разряда в воздухе", страница 2

,

где е — основание натурального логарифма. Таким образом, максимальное значение α при заданной напряженности электрического поля Е пропорционально этой напряженности. Опыт подтверждает и эту зависимость.

Выражение (2) одна из наиболее распространенных аппроксима­ций при аналитическом представлении результатов экспе­риментальных измерений коэффициента а. Из  этой зависимости для а крите­рий пробоя имеет вид:

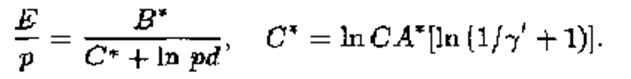   (4)

Выражение (4) описывает т.н. кривые Пашена (рис. 1 ), связывающие р, dи Е (или ) у порога пробоя.

Кривые Пашена получены эмпирически для раз­личных газов и материалов катода.

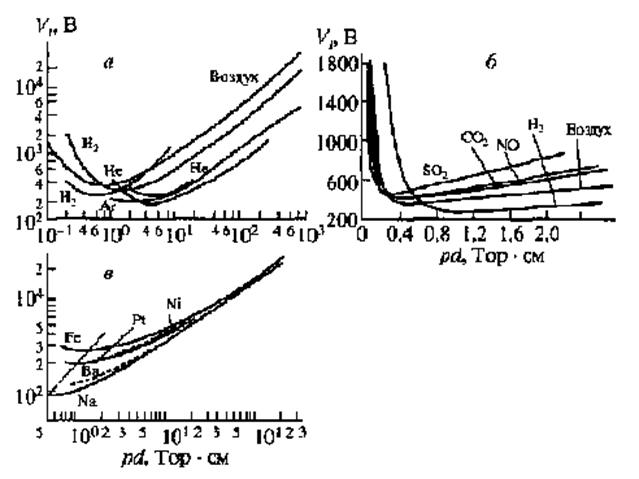
Рис. 1. Кривые Пашена: а — потенциал зажигания в различных газах в широком диапазоне значений pd;  б — кривые Пашена в укрупненном масштабе; в — влияние материала катода на напряжение пробоя аргона. Штрихпунктирная прямая соединяет точки минимума. Ее наклон 45° соот­ветствует независимостиот материала катода

Минимальное значение пробойного напряжения:

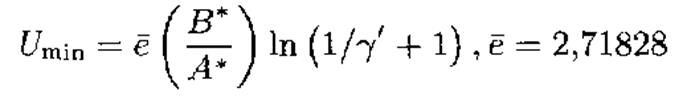
достигается при

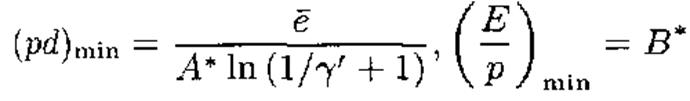
Припробой затрудняется уменьшением числа встречаемых электроном нейтральных частиц, при — уменьшением длины набора энергии между столкновениями.

Разумеется, все выведенные соотношения справедливы и для положительных ионов.

Возникновение лавины - это еще не пробой. Необходимо, чтобы после прохождения лавины на катоде снова появился электрон. После этого возникает повторная лавина, затем еще лавина и т.д. Возникает самостоятельный многолавинный разряд. Для самостоятельности разряда необходимо вырывание электронов из катода положительными ионами, либо фотонами. Для оценки процесса вводят коэффициент g - так называемый вторичный ионизационный коэффициент. Для плотности электронного тока в определенных условиях можно получить выражение .

Как отмечалось выше, условием самостоятельности разряда является появление на катоде хотя бы одного электрона после прохождения лавины:

1-g(e^ad-1) = 0

Обратимся теперь к условию зажигания разряда. Для простоты предположим, что вторичная эмиссия электронов с катода роли не играет (γ = 0). Тогда условие переходит в

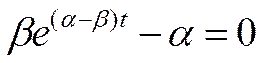
Подставим сюда

             

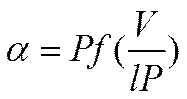
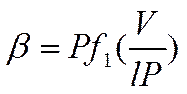
где V – напряжение на

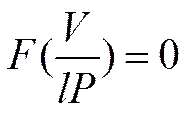
где F - некоторая функция аргумента V/(lP). Решая это уравне­ние, найдем «потенциал зажигания» V_заж — V_заж (lP). Отсюда следует, что разность потенциалов между электродами трубки, при которой начинается пробой газа, есть функция произведения давления газа P на расстояние между электродами. Если в несколь­ких разрядных трубках с плоскими электродами создать условия, при которых произведения Pl постоянны, то для всех трубок по­требуется одна и та же разность потенциалов, чтобы вызвать газо­вый разряд. Этот закон был установлен экспериментально Пашеном (1865 - 1947) еще до создания Таунсендом теории пробоя газа. При высоких давлениях газа (порядка сотен атмосфер) наблюдаются отступления от за­кона Пашена.

Для однородного поля можно вывести уравнение зависимости пробивного напряжения от произведения рd вида U_пр = f(pd), которое носит название закона Пашена.

(5)

где A и B - постоянные, характеризующие газ.

Эксперименты для разных газов дают хорошее совпадение с такой зависимостью. В полном соответствии с этой формулой и экспериментальными данными получено простое уравнение для расчета пробивного напряжения в воздухе при давлении, близком атмосферному:

(6)

где р - давление газа, атм; d - расстояние между электродами, см; U - в кВ.

Зависимость для воздуха, соответствующая (5)  приведена на рис. 2.

Рис. 2. Зависимость пробивного напряжения в воздухе в однородном поле от произведенияpd(закон Пашена)

При определении межэлектродного расстояния в газе, обеспечивающего заданную электрическую прочность, необходимо учитывать целый ряд влияющих факторов. Основные из них — это форма электрического поля в промежутке, вид воздействующего напряжения, род газа и его плотность.